Question

If $n\sin x={\log }_{e}x$ has exactly 1 root, then find the possible value of $n(n\in N)$.

Explanation

`nsinx=log_(e)x`
`impliessinx=(log_(e)x)/(n)`
For exactly one root, the graph of `y=sinx` must intersect the graph of `y=(log_(e)x)/(n)` exactly once.
Maximum value of sin x is 1.

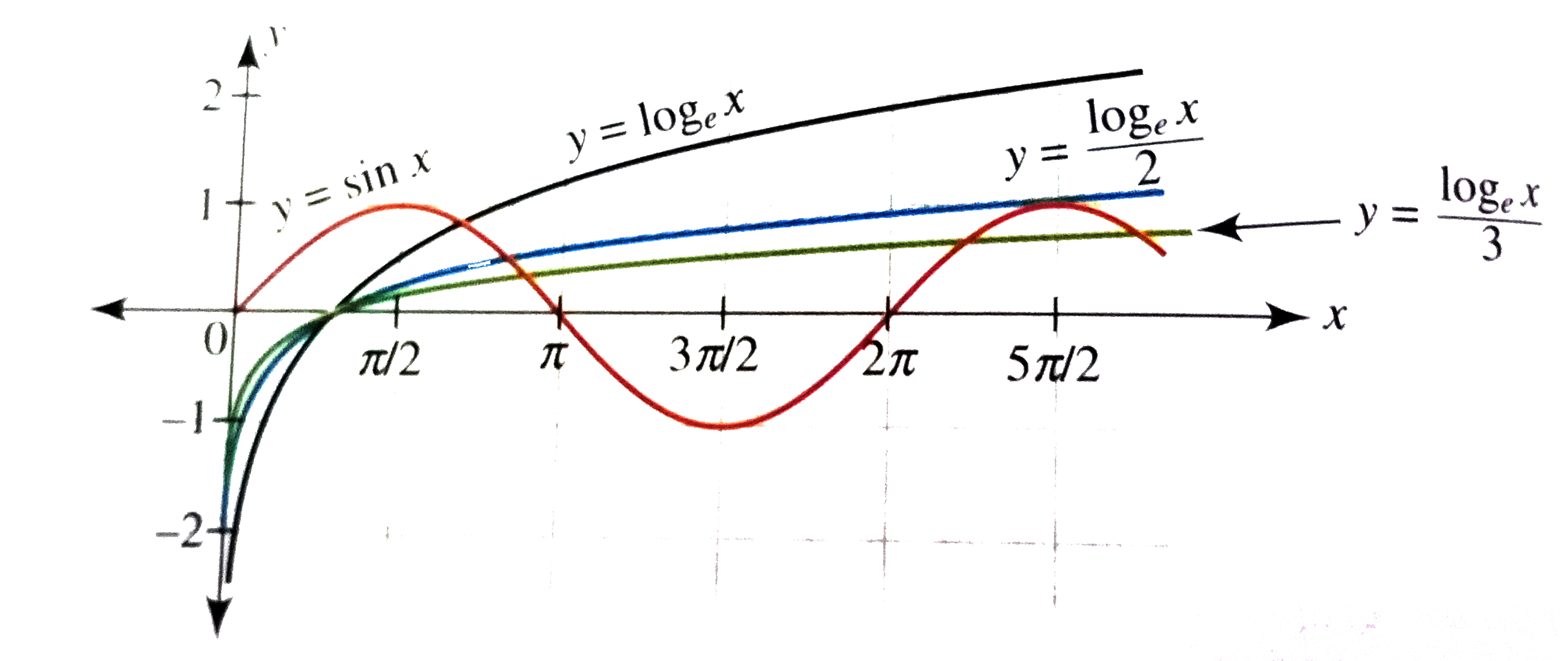
For `n=1,sinx=log_(e)x`
Graphs of `y=sinxandy=log_(e)x` intersect only once as shown in the following figure. For `x=e,log_(e)e=1`, hence after `x=e,y=log_(e)x` never meets `y=sinx`.
For `n=2,"let"(log_(e)x)/(2)=1:.log_(e)x=2orx=e^(2)lt5pi//2`
Hence the graph of `y=(log_(e)x)/(2)` meets `y=sinx` only once.
But for `n=3and(log_(e)x)/(3)=1,x=e^(2)gt5pi//2` hence the graph of `y=(log_(e)x)/(3)` meet the graph of `y=sinx` more than once.
So for exactlly one root of the equation `sinx=(log_(e)x)/(n),n=1or2`.