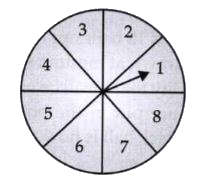
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2,3,4,5,6,1,8 (see Figure), and these are equally likely outcomes. What is the probability that it will point at(i) 8?(ii) an odd number?(iii) a number greater than 2?(iv) a number less than 9?
Here, sample space, S={1,2,3,4,5,6,7,8}
So, n(S)=8
As, pointing a number are equally likely outcomes, so, pointing a number will have a probability of 18.
(i) From above, we can say that arrow pointing at number 8 will have a probability of 18.
(ii)Odd numbers in given sample space, Eo={1,3,5,7}
So,n(Eo)=4
Probability of arrow pointing at odd number, P(Eo)=48=12
(iii)Number greater than 2,Eg={3,4,5,6,7,8}
So,n(Eg)=6
Probability of arrow pointing a number greater than 2, P(Eg)=68=34
(iii)Number less than 9,El={1,2,3,4,5,6,7,8}
So,n(El)=6
Probability of arrow pointing a number less than 9, P(El)=88=1
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - Exercise 15.25videos
PROBABILITY
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - SOLVED EXAMPLES13videos
PROBABILITY
- BOOK - NCERTCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.45videos
POLYNOMIALS
- BOOK - NCERTCHAPTER - QUADRATIC EQUATIONSEXERCISE - EXERCISE 4.26videos
QUADRATIC EQUATIONS
Similar Questions
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see figure) and these are equally likely outcomes. What is the probability that it will point at :
(i) 8? (ii) an odd number?
(iii) a number greater than 2? (iv) a number less 9?View SolutionA game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (See Fig. 131), and these are equally likely outcomes. What is the probability that it will point at (i) 8? (ii) an odd number? (iii) a number greater than 2? (iv) a number less than 9?
View Solution
Knowledge Check
- Question 1 - Select One
A game of chance consists of spinning an arrow, which comes to rest pointing at one of the numbers 1,2,3,4,5,6,7,8 and these are equally likely outcomes. Find the probability that the arrow will point at any factor of 8.
A58B78C18D38
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2 3,4,5,6,7,8 and these are equally likely outcomes what is the probability that it will point at :
(i) 8?
(ii) an odd number ?
(iii) a number greater than 2 ?
(iv) a number less than 9 ?View SolutionRead the following text and answer the following question on the basis of the same.
A game of chances consisting of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see the figure) and these are equally likely outcomes.
What is the probability that it will point at a number greater than 2?View SolutionA game of chance consist of spinning an arrow which comes to rest pointing at one of the numbers 15,20,25,30,35,40,45,50 and these are equally likely outcomes. What is the probability that it will point at
(i) an even number? (ii) at a number multiple of 5
(iii) at a number divisible by 3 (iv) at a prime number.View SolutionA game of chance consists of spinning an arrow on a circular board, divided into 8 equal parts, which comes to rest pointing at one of the numbers 1,2, 3, ..., 8 , which are equally likely outcomes. What is the probability that the arrow will point at (i) an odd numbei ? (ii) a number greater than 3? (Hi) a number less than 9?
 View Solution
View SolutionRead the following text and answer the following question on the basis of the same.
A game of chances consisting of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see the figure) and these are equally likely outcomes.
What is the probability that arrow point lies on the odd number?View SolutionA game of chance consists of spinning an arrow on a circular board , divided into 8 equal parts , which comes to rest pointing at one of the numbers 1,2,3,…..8 which are equally likely outcomes . What is the probability that the arrow will point
(a) at an odd number
(b) a number greater than 3
(c ) a number less than 9 .
 View Solution
View SolutionIn a game of chance, a spining arrow comes to rest at one of the numbers
1,2,3,4,5,6,7,8,
All these are equally likely outcomes.
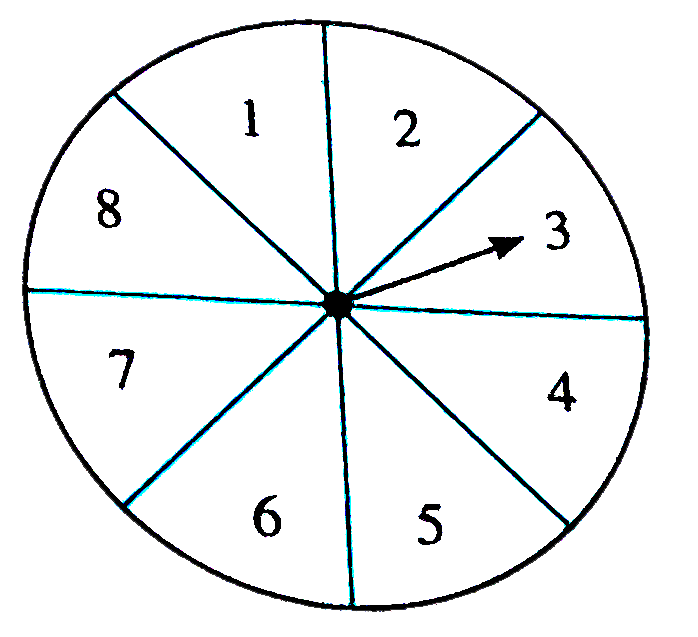
Find the probability that it will rest atView Solution

