Find the equation of the projection of the line $\frac{x - 1}{2} = \frac{y + 1}{- 1} = \frac{z - 3}{4}$ on the plane $x + 2 y + z = 9 .$

Video Solution

Text Solution

Verified by Experts

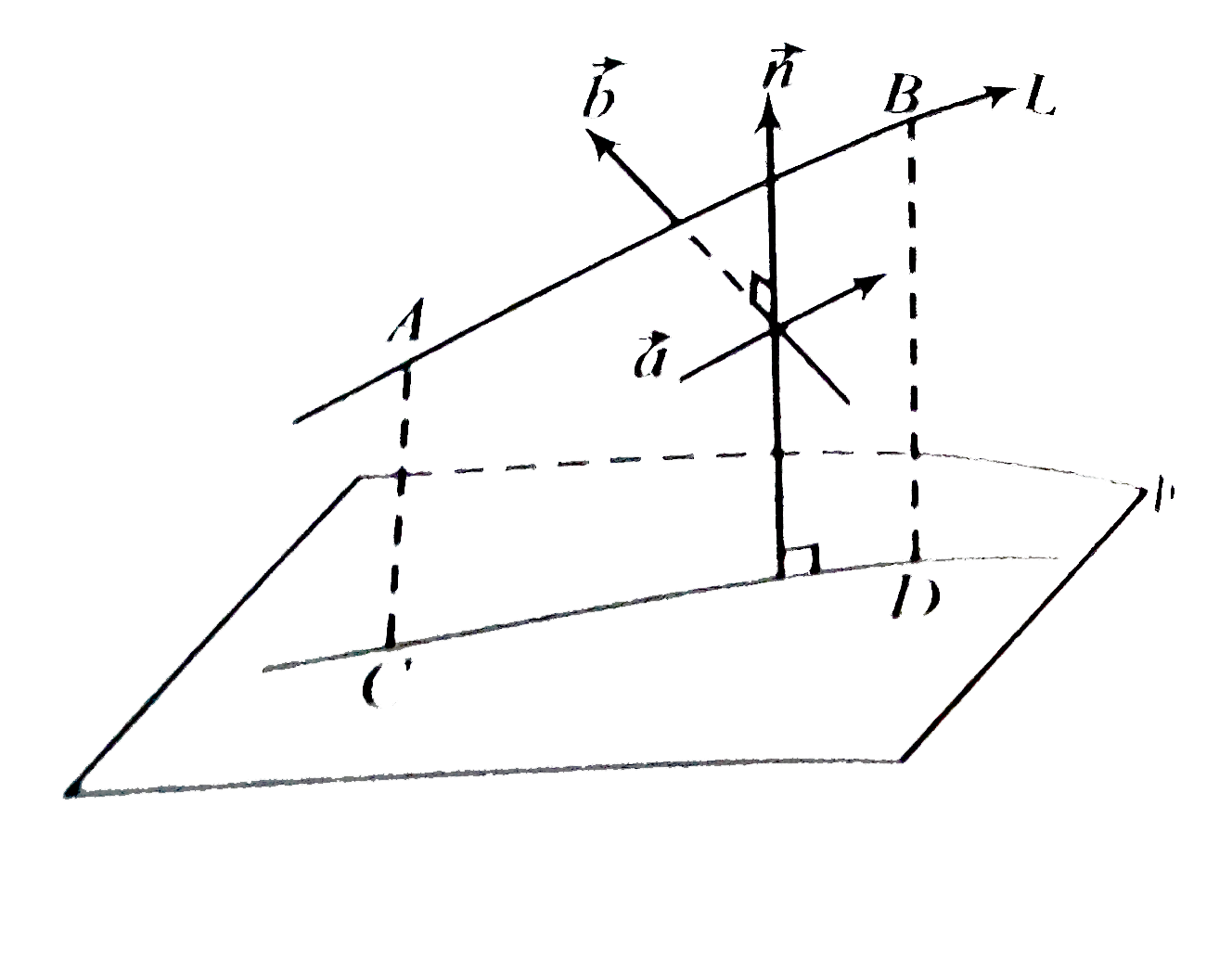
Projection of given line $L \equiv \frac{x - 1}{2} = \frac{y + 1}{- 1} = \frac{z - 3}{4}$ on given plane $P \equiv x + 2 y + z = 9$ is the line of intersection of plane P and plane (ABCD) through the line L and perpendicular to the plane P.
Now line L is parallel to vector $\to a = 2 ˆ i - ˆ j + 4 ˆ k$ .
Vector normal to plane $P$ is $\to n = ˆ i + 2 ˆ j + ˆ k$ (ii)
$∴$ Vector normal plane ABCD is $\to b = \to a \times \to n = ∣ ∣ ∣ ∣ ∣ \begin{matrix} ˆ i & ˆ j & ˆ k 2 & - 1 & 4 1 & 2 & 1 \end{matrix} ∣ ∣ ∣ ∣ ∣ = - 9 ˆ i + 2 ˆ j + 5 ˆ k$
Plane ABCD passes through the line L, i.e., passes through the point (1, -1, 3). Thus,
Equation of plane $A B C D = (- 9) (x - 1) + 2 (y + 1) + 5 (z - 3) = 0 or 9 x - 2 y - 5 z + 4 = 0$ (iii)
Now required projection is line of intersection of given plane P and plane ABCD
or $x + 2 y + z - 9 = 9 x - 2 y - 5 z + 4$

Updated on:21/07/2023

The equation of the projection line of the line $\frac{x + 1}{2} = \frac{y + 1}{- 1} = \frac{z + 3}{4}$ on the plane $x + 2 y + z = 6$ is
A $\frac{x - 1}{4} = \frac{y - 3}{7} = \frac{z - 1}{10}$
B $\frac{x - 1}{- 4} = \frac{y + 3}{7} = \frac{z - 1}{10}$
C $\frac{x - 1}{4} = \frac{y - 3}{- 7} = \frac{z + 1}{10}$
D $\frac{x + 3}{4} = \frac{y - 2}{7} = \frac{z - 7}{- 10}$
Point of intersection of the line
$\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z + 3}{4}$ and the plane 2x+4y -z=1 is
A $(- 1, - 1, - 7)$
B(1,-1,7)
C(1,1,7)
D(1,1,-7)
Equation of line of projection of the line $3 x - y + 2 z - 1 = 0 = x + 2 y - z = 2$ on the plane $3 x + 2 y + z = 0$ is
A $\frac{x + 1}{11} = \frac{y - 1}{- 9} = \frac{z - 1}{- 15}$
B $3 x - 8 y + 7 z + 4 = 0 = 3 x + 2 y + z$
C $\frac{x + 12}{11} = \frac{y + 8}{- 9} = \frac{z + 14}{15}$
D $\frac{x + 12}{11} = \frac{y + 8}{- 9} = \frac{z + 14}{- 15}$