Let PM be the perpendicular from the point P(1,2,3) to the x−y plane. If −−→OP makes an angle θ with the positive direction of the z− axis and −−→OM makes an angle φ with the positive direction of x− axis, where O is the origin and θ and φ are acute angels, then If f(x+y)=f(x)+f(y)−xy−1, ∀x,y in R andf(1)=1,thentheνmberofsolutionoff(n)=n,n in N , is
cosθcosϕ=1√14, tanϕ=2, tanθ=√53
sinθsinϕ=2√14, tanϕ=2, tanθ=√53
tanϕ=2, cosθcosϕ=1√14, tanθ=√53
tanθ=√53, cosθcosϕ=1√14, tanϕ=2
The correct Answer is:B
If P be (x,y,z), then from the figure,
x=rsinθcosϕ,y=rsinθsinϕandz=rcosθ
1=rsinθcosϕ,2=rsinθsinϕand3=rcosθ
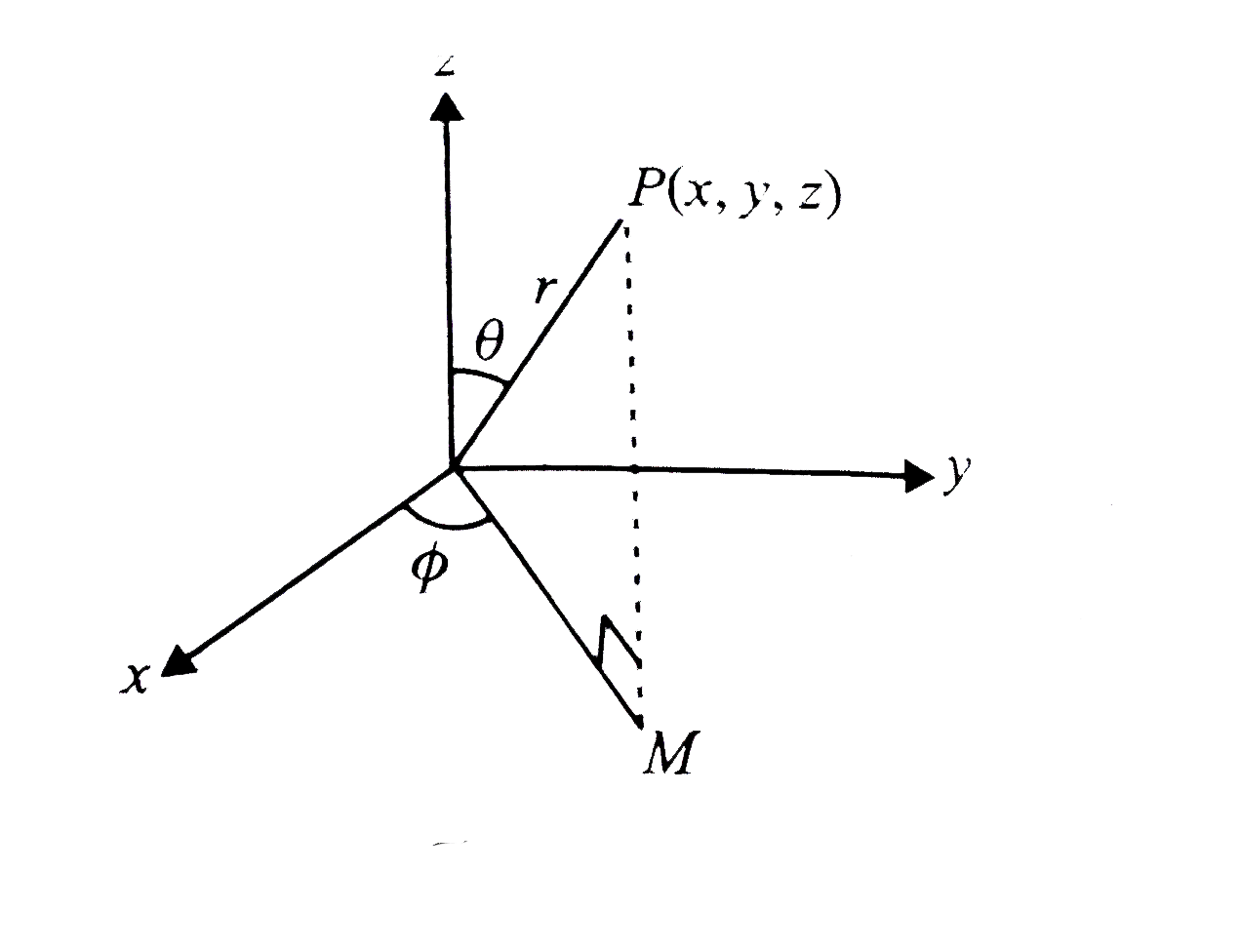
⇒ 12+22+32=r2orr=±√14
∴ sinθcosϕ=1√14,sinθsinϕ
=2√14andcosθ=3√14
(neglecting negative sign as θandϕ are acute)
sinθsinϕsinθcosϕ=21ortanϕ=2
Also, tanθ=√5/3.
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Reasoning Questions)
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Comprehension)
12 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Single)
86 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
20 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
34 Videos
Similar Questions
Let PM be the perpendicular from the point P(1,2,3) to XY-plane. If OP makes an angle θ with the positive direction of the Z-axies and OM makes an angle Φ with the positive direction of X-axis, where O is the origin, then find θandΦ.
View SolutionLet PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle ϕ with the positive direction of x− axis, whereO is the origin and θandϕ are acute angels, then a. cosθcosϕ=1/√14 b. sinθsinϕ=2/√14 c. tanϕ=2 d. tanθ=√5/3
View Solution
Knowledge Check
Let PM be the perpendicular from the point P(1,2,3) to XY-plane. If OP makes an angle θ with the positive direction of the Z-axies and OM makes an angle Φ with the positive direction of X-axis, where O is the origin, θandΦ are acute angles, then
Atan(θ)=√53Bsin(θ)sin(ϕ)=2√14Ctan(θ)=2Dcos(θ)cos(ϕ)=1√14Let PN be the perpendicular from the point
P(1,2,3) to xy-plane. If OP makes an angle α
with positive direction of the z-axis and ON makes
an angle β with the positive direction of x-axis,
where O is the origin (αandβ are acute angles),
thenAsinαsinβ=2√14Bcosαcosβ=2√14Ctanα=√53Dtanβ=2If f(x) is a real valued functions satisfying f(x+y)=f(x)+f(y)−yx−1 for all x,y∈R such that f(1)=1 then the number of solutions of f(n)=n,n∈N, is
A1B2C3D4
Let PQ be the perpendicular form P(1,2,3) to xy-plane. If OP makes an angle theta with the positive direction of z-axis and OQ makes an angle ϕ with the positive direction of x-axis where O is the origin show that tanθ=√53andtanϕ=2.
View Solutionf(xy)=f(x)−f(y)∀x,y∈R+andf(1)=1, then show that f(x)=Inx.
View SolutionLet f(x+y)+f(x−y)=2f(x)f(y)∀x,y∈R and f(0)=k, then
View SolutionIf f(x+y)=f(x)+f(y)−xy−1∀x,y∈Randf(1)=1, then the number of solution of f(n)=n,n∈N, is 0 (b) 1 (c) 2 (d) more than 2
View SolutionIf f(x+y)=f(x)+f(y)−xy−1 for all x,y∈R and f(1)=1 then f(n)=n,n∈N is true if
View Solution
