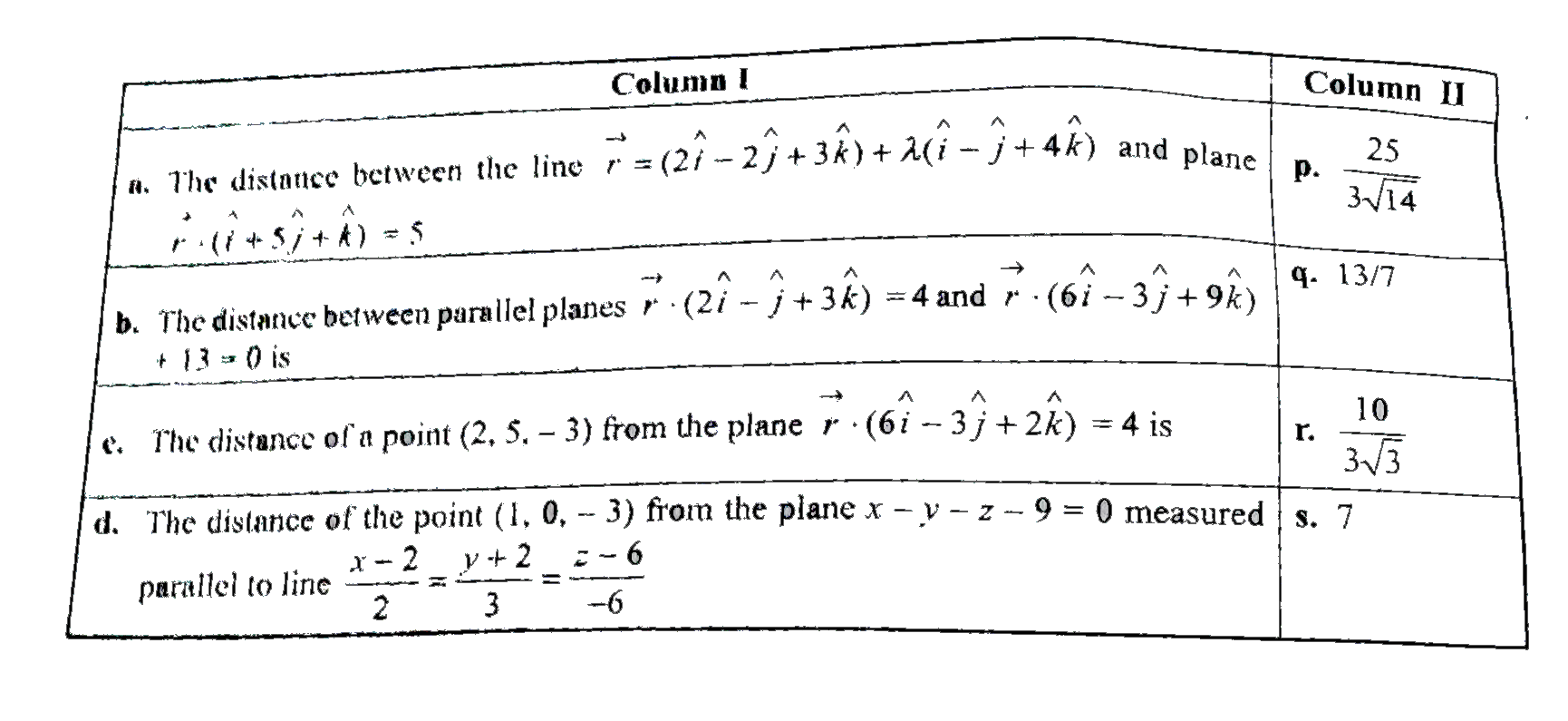The correct Answer is:a→r;b→p;c→q;d→s
The given line and plane are →r=(2ˆi−2ˆj+3ˆk)+λ(ˆi−ˆj+4ˆk)and→r⋅(ˆi+5ˆj+ˆk)=5, respectively. Since (ˆi−ˆj+4ˆk)⋅(ˆi+5ˆj+ˆk)=0, line and plane are parallel.
Hence, the required distance is equal to distance of point (2,−2,3) from the plane x+5y+z−5=0, which is |2−10+3−5|√1+25+1=103√3
b. The distance between two parallel planes →r⋅(2i−j+3k)=4and→r⋅(6i−3j+9k)+13=0 is
d=|4−(−13/3)|√(2)2+(−1)2+(3)2=(25/3)√14
=253√14
c. The perpendicular distance of the point (2,5,−3) fromt the plane →r⋅(6i−3j+2k)=4or6x−3y+2z−4=0 is
d=|12−15−6−4|√36+9+4
=13/√49=13/7
d. The equation of the line AB is
x−22=y+23=z−6−6
The equation of line passing through (1,0,−3) and parallel to AB is
x−12=y3=z+3−6=r (say)
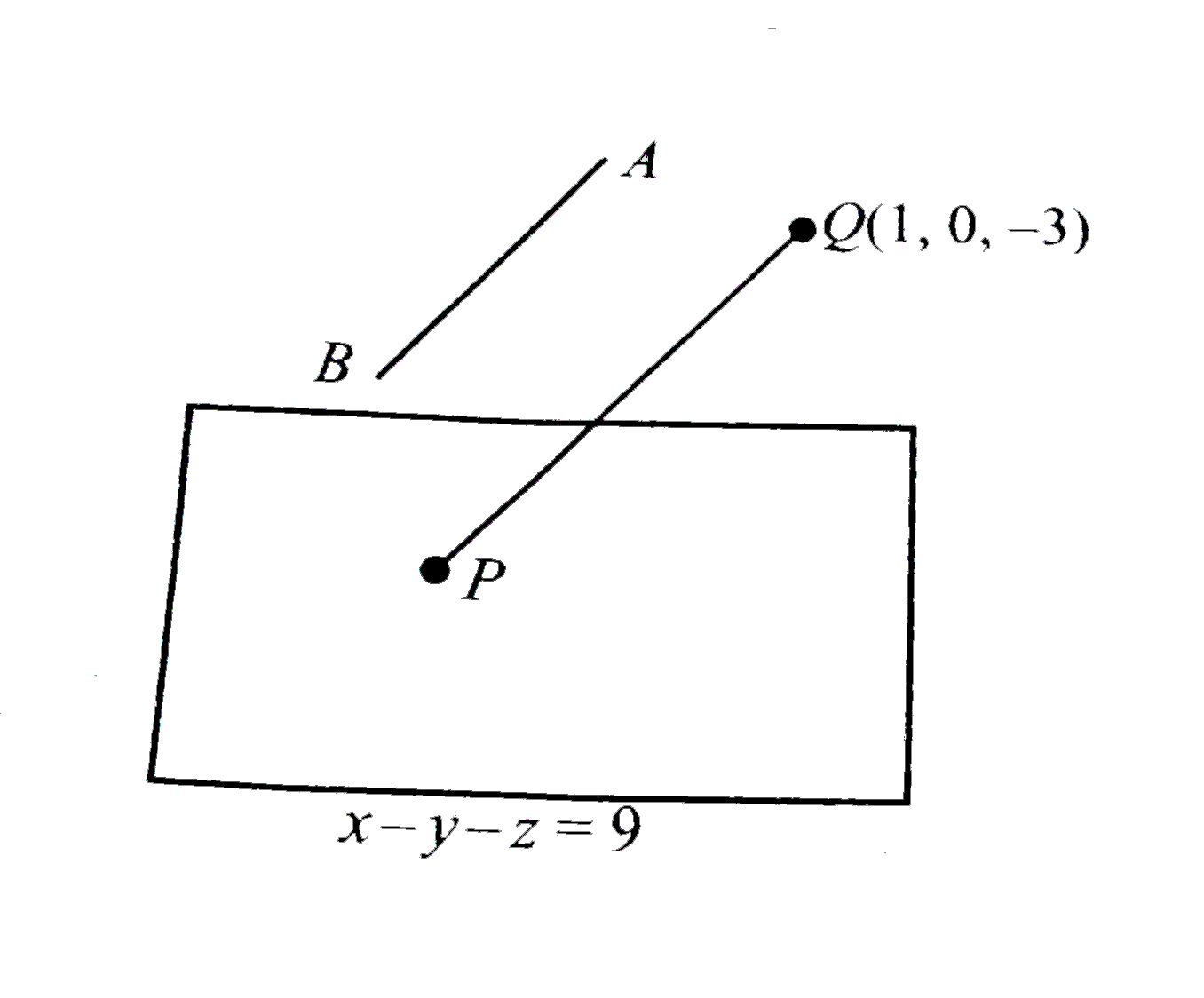
The coordinates of any point on line P(2r+1,3r,−6r−3) which lie on plane
(2r+1)−(3r)−(−6r−3)=9
r=1
Point P≡(3,3,−9)
Required distance
PQ=√(3−1)2+(3−0)2+(−9+3)2
=√4=9+36=7
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Numerical)
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - JEE Previous Year
26 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Comprehension)
12 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
20 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
34 Videos
Similar Questions
Find the number of sphere of radius r touching the coordinate axes.
View Solution(i) Find the equation of the plane passing through the points(2,1,0),(5,0,1)and(4,11). (ii) If P s the point (2,1,6), then the find the point Q such that PQ is perpendicular to the plane in (i) and the midpoint of PQ lies on it.
View SolutionGiven four points A(2,1,0),B(1,0,1),C(3,0,1)andD(0,0,2). Point D lies on a line L orthogonal to the plane determined by the points A, B and C.
The equation of the plane ABC is
View SolutionLet the line L1:x−12=y−23=z−34 and L2:x−21=y−32=z−k4 intersect at P.The least distance of P from the plane 3x−4y−12z+4=0, equals
View SolutionNumber of solutions of the equation
sin7θ=sinθ+sin3θ∈0<θ<π2 is equal to
View SolutionIdentify the cell organelle 'A' :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_BIO_C10_E08_018_Q01.png" width="80%"gt
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
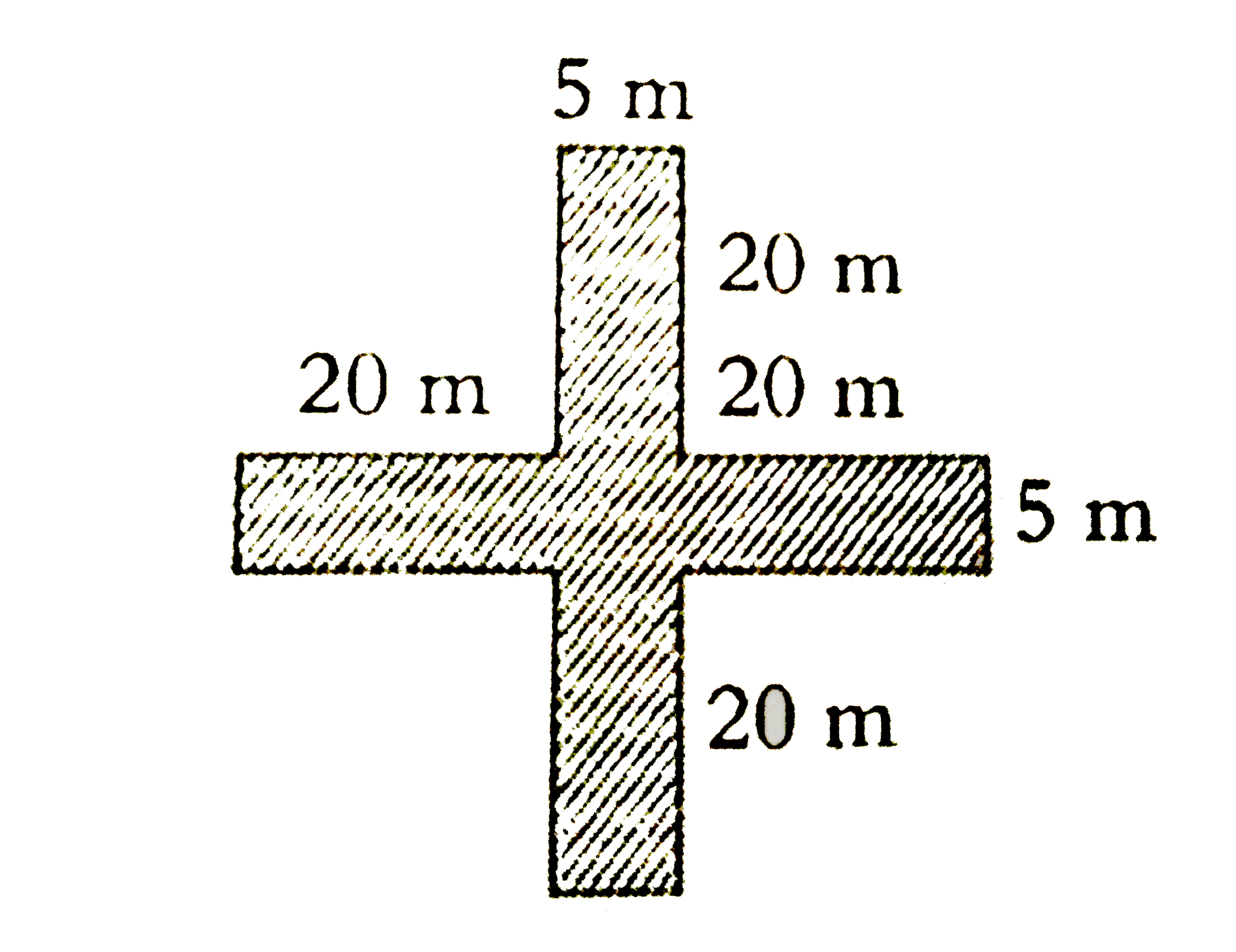
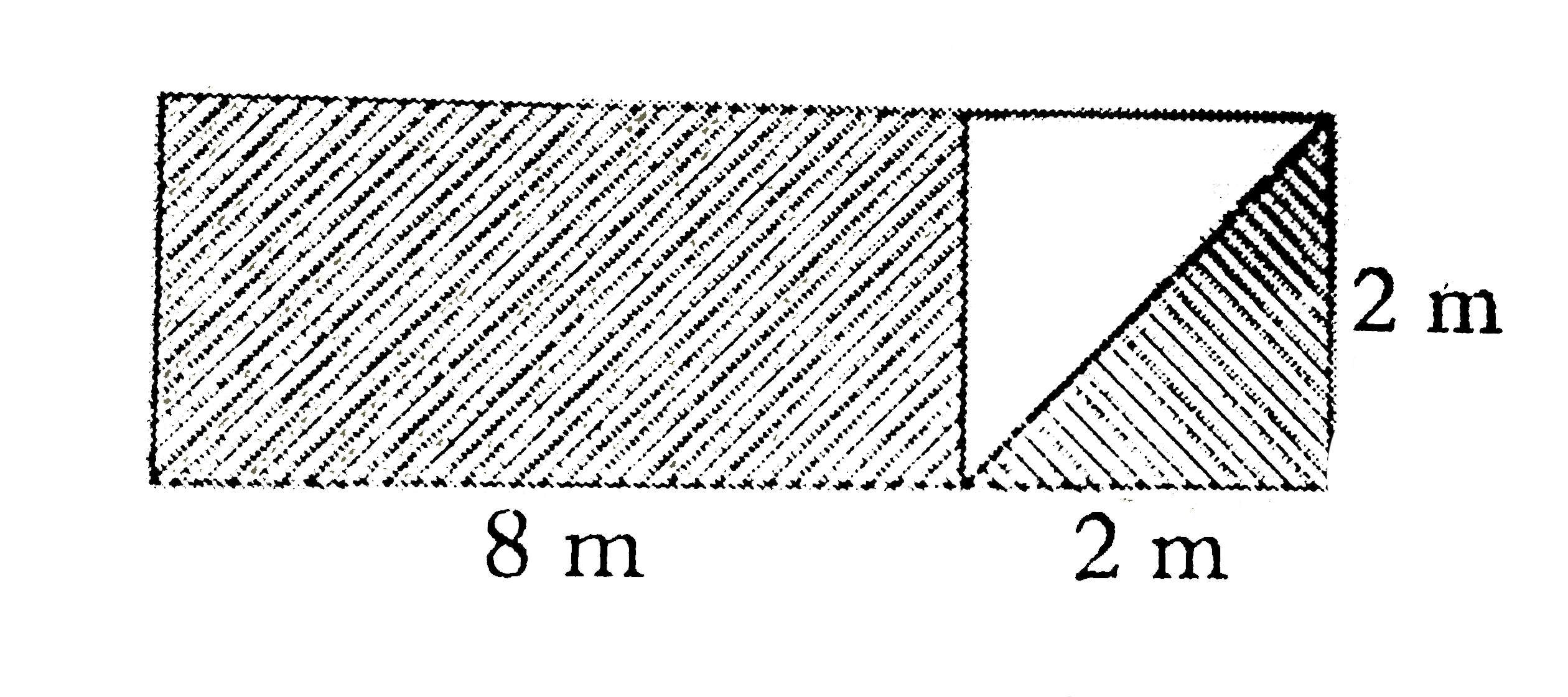
View SolutionThe area of the shaded part in the figure given below is ______.
View SolutionThe inequation represented by the graph given below is :
View Solution