Consider a pyramid OPQRS located in the first octant $(x \geq 0, y \geq 0, z \geq 0)$ with O as origin, and OP and OR along the x-axis and the y-axis,respectively. The base OPQR of the pyramid is asqu are with $O P = 3$ . The point S is directly above the mid-point T of diagonal OQ such that $T S = 3$ .Then

A

the acute angle between OQ and OS is $π / 3$

B

the equataion of the plane containing th etriangle OQS is x-y=0

C

the length of the perpendicular from P to the plane containing the triagle OQS is $\frac{3}{\sqrt{2}}$

D

the perpendcular distance from O to the straight line containing RS is $\sqrt{\frac{15}{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:b.,c.,d

b.,c.,d
Direction rations of $O Q \equiv (3, 3, 0)$
Direction rations of $O S \equiv (\frac{3}{2}, \frac{3}{2}, 3)$
if $θ$ is the angle between OS and OR , then
$cos θ = \frac{3 \times \frac{3}{2} + 3 \times \frac{3}{2}}{\sqrt{3^{2} + 3^{2}} \sqrt{{(\frac{3}{2})}^{2} + {(\frac{3}{2})}^{2} + 3^{2}}} = \frac{1}{\sqrt{3}}$

$∴$ hence (a) is wrong
Normal t plane OQS,
$- - \to O Q \times - - \to O S = \pm ∣ ∣ ∣ ∣ ∣ \begin{matrix} ˆ i & ˆ j & ˆ k 3 & 3 & 0 \frac{3}{2} & \frac{3}{2} & 3 \end{matrix} ∣ ∣ ∣ ∣ ∣ = \pm (9 ˆ i - 9 ˆ j)$
$∴$ Equation of plane OQS is
$(x ˆ i + y ˆ j + z ˆ k) . (9 ˆ i - 9 ˆ j) = 0$
$\Rightarrow x - y = 0$
Distance of p from plane OQS = distancae PT = distance OT $= \frac{3}{\sqrt{2}}$
Equation of RS is $\frac{x - 0}{\frac{3}{2} - 0} = \frac{y - 3}{\frac{3}{2} - 3} = \frac{z - 0}{3 - 0}$
$or \frac{x}{\frac{3}{2}} = \frac{y - 3}{- \frac{3}{2}} = \frac{z}{3}$

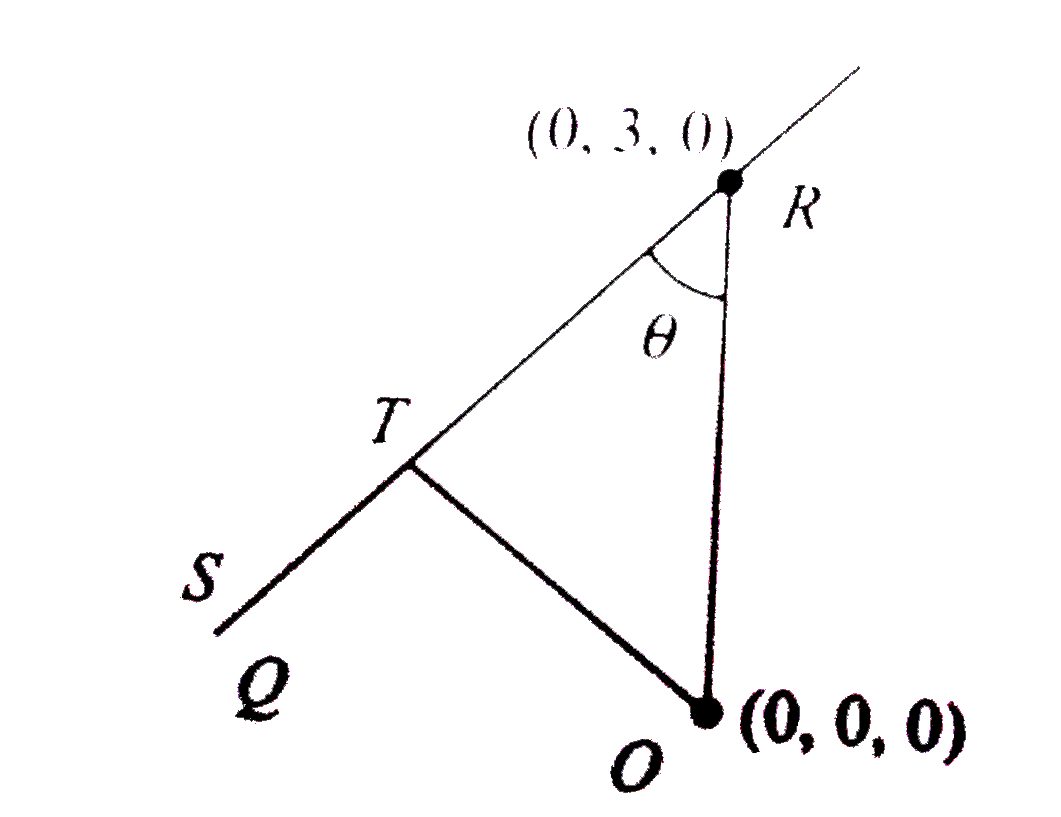
ANgle between line Rs and OR
$cos θ = \frac{0 + 3 (- \frac{3}{2}) + 0}{3 \sqrt{{(\frac{3}{2})}^{2} + {(\frac{3}{2})}^{2} + 3^{2}}} = - \frac{1}{\sqrt{6}}$
distance $= O T = O R sin θ = 3 \sqrt{1 - \frac{1}{6}} = 3 \sqrt{\frac{5}{6}} = \sqrt{\frac{15}{2}}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Consider a pyramid OPQRS located in the first octant $(x \geq 0, y \geq 0, z \geq 0)$ with O as origin and OP and OR along the X-axis and the Y-axis , respectively. The base OPQRS of the pyramid is a square with OP=3. The point S is directly above the mid point T of diagonal OQ such that TS=3. Then,
A1.the acute angle between OQ and OS is $π / 3$
B2.the equataion of the plane containing th etriangle OQS is x-y=0
C3.the length of the perpendicular from P to the plane containing the triagle OQS is $\frac{3}{\sqrt{2}}$
D4.the perpendcular distance from O to the straight line containing RS is $\sqrt{\frac{15}{2}}$
Question 2 - Select One
Consider a pyamid OPQRS locaated in the first octant $(x \geq 0, y \leq 0, z \leq 0)$ with O as origin , and OP an OR along the x-axis and y-axis respectively. The base OPQR of the pyramid is a square with OP=3 . The point S is directly above the mid-point T of the diagonal OQ such that TS=3 , Then , the angle between OQ and OS, is
A $\frac{π}{3}$
B $\frac{π}{6}$
C ${cos}^{- 1} \frac{1}{\sqrt{3}}$
D ${cos}^{- 1} \frac{1}{3}$
Question 3 - Select One
If a line OP through the origin O makes angles $α, 45^{\circ} and 60^{\circ}$ with x, y and z axis respectively then the direction cosines of OP are.
A $\frac{1}{\sqrt{2}}, \frac{1}{2}, \frac{1}{2}$
B $\frac{1}{2}, \frac{1}{2}, \frac{1}{\sqrt{2}}$
C $\frac{1}{2}, \frac{1}{\sqrt{2}}, \frac{1}{2}$
Dnone of these

CENGAGE-JEE 2019-multiple correct answers type

Consider a pyramid OPQRS located in the first octant (x >= 0, y >= 0, ...
15:12

Home
Ask Doubt
Profile