The mass of gas adsorbed , x , per unit mass of adsorbate , m , was measured at various pressures , p . A graph between log xm and log p gives a straight line with slope equal to 2 and the intercept equal to 0.4771 .The value of xm at a pressure of 4 atm is : (Given log 3 = 0.4771)
To solve the problem, we will use the Freundlich adsorption isotherm equation, which can be expressed in logarithmic form. Here are the steps to find the value of xm at a pressure of 4 atm.
Step 1: Understand the Freundlich Adsorption Isotherm
The Freundlich adsorption isotherm is given by:
xm=kp1n
where:
- xm is the mass of gas adsorbed per unit mass of adsorbate,
- p is the pressure,
- k is a constant,
- n is a constant related to the adsorption intensity.
Step 2: Convert to Logarithmic Form
Taking the logarithm of both sides gives:
log(xm)=log(k)+1nlog(p)
This is in the form of a straight line y=mx+c, where:
- y=log(xm),
- m=1n,
- x=log(p),
- c=log(k).
Step 3: Identify the Slope and Intercept
From the problem, we know:
- The slope m=2 (which means 1n=2),
- The intercept c=0.4771.
Step 4: Calculate n
From the slope:
1n=2⟹n=12=0.5
Step 5: Calculate k
The intercept gives us:
log(k)=0.4771
To find k, we take the antilogarithm:
k=100.4771
Given that log(3)=0.4771, we have:
k=3
Step 6: Substitute Values to Find xm at p=4atm
Now we can substitute p=4atm into the Freundlich equation:
xm=kp1n=3⋅42
Calculating 42:
42=16
Thus:
xm=3⋅16=48
Final Answer
The value of xm at a pressure of 4 atm is 48.
---
The Freundlich adsorption isotherm is given by:
xm=kp1n
where:
- xm is the mass of gas adsorbed per unit mass of adsorbate,
- p is the pressure,
- k is a constant,
- n is a constant related to the adsorption intensity.
Taking the logarithm of both sides gives:
log(xm)=log(k)+1nlog(p)
This is in the form of a straight line y=mx+c, where:
- y=log(xm),
- m=1n,
- x=log(p),
- c=log(k).
From the problem, we know:
- The slope m=2 (which means 1n=2),
- The intercept c=0.4771.
From the slope:
1n=2⟹n=12=0.5
The intercept gives us:
log(k)=0.4771
To find k, we take the antilogarithm:
k=100.4771
Given that log(3)=0.4771, we have:
k=3
Now we can substitute p=4atm into the Freundlich equation:
xm=kp1n=3⋅42
Calculating 42:
42=16
Thus:
xm=3⋅16=48
The value of xm at a pressure of 4 atm is 48.
Topper's Solved these Questions
Similar Questions
Graph between log(xm) and logP is straight line at angle of 45∘ with the intercept of 0.6020.
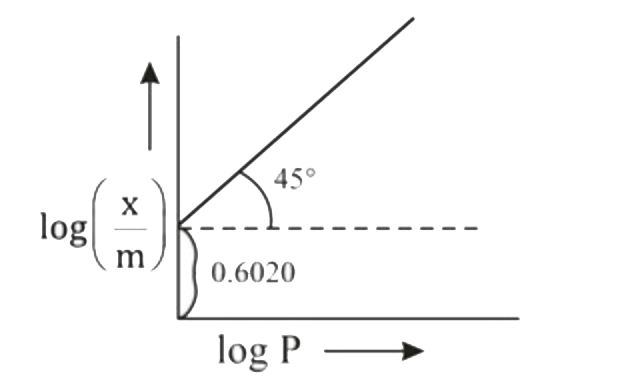
The extent of adsorption (xm) at a pressure of 1 atm is
View SolutionA graph between log (x/m) and log p is straight line at an angle of 45∘ with intercept on y-axis equal to 0.3010. Calculate the amount of the gas adsorbed per gram of the adsobent when the pressure is 0.2 atm.
View Solution
Knowledge Check
A plot of x/m versus log p for the adsorption of a gas on a solid gives a straight line with slope equal to
A1/nBlog kC−logkDn.A plot of log x/m versus log p for the adsorption of a gas on a solid gives a straight line with slope equal to:
A– log KBnC1nDLog KA plt of log Xm vs. log P for the adsorption of a gasd on a solid gives a straight line with slope equal to :
A1/nBlnKC−logKDn
Graph between log(x/m) vs logP has a slope=2 and intercept = 0.477. Find (x/m) at pressure 4 atm.
View SolutionGraph between log x/m and log P is a straight line at angle of 45∘ with intercept 0.4771 on y-axis. Calculate the amount of gas adsorbed in gram per gram of adsorbent when pressure is 3 atm.
View SolutionIf a graph is plotted between log(a−x) and t, the slope of the straight line is equal to −0.03. The specific reaction rate will be
View SolutionIn an adsorption experiment, a graph of log(x/m) versus log P was found to be linear with a slope of 45°, and the the intercept of of 0.3010. The amount of gas adsorbed per gram charcoal under a pressure of 0.8 bar is
View SolutionA plot of log (x/m) versus log p for the adsorption of a gas on the surface of a solid gives a straight line which slope equal to :
View Solution
