A cone of equal height and equal base is cut off from a cylinder of height 24 cm and base radius 7 cm .Find the total surface and volume of remaining solid.

Text Solution

Verified by Experts

Here r=7 cm,h =24 cm
volume of remaining solid =volume of cylinder -volume of cone
$= π r^{2} h - \frac{1}{3} π^{2} h = \frac{2}{3} π r^{2} h$
$= \frac{2}{3} \times \frac{22}{7} \times 7 \times 24 = 2464 c m^{3}$ ltbr Noo , l^(2)=h^(2)+r^(2)=(24)^(2)+(7)^(2) $< b r >$ =576+49=625 $< b r > l = 25 c m < b r > T o t a l s u r f a c e a r e a o f r e m a \in \in g s o l b r > = c u r v e d s u r f a c e o f c y l \in d e r + c u r v e d s u r f a c e o f c o \neq + a r e a o f ⊤ < b r >$ =2pirh+pirl+pir^(2) $< b r >$ =pir(2h+l+r) $< b r >$ 1=(22)/(7)xx7(2xx24+25+7)=22xx80=1760 cm^(2)

|

Updated on:21/07/2023

Class 10 MATHS SURFACE AREAS AND VOLUMES

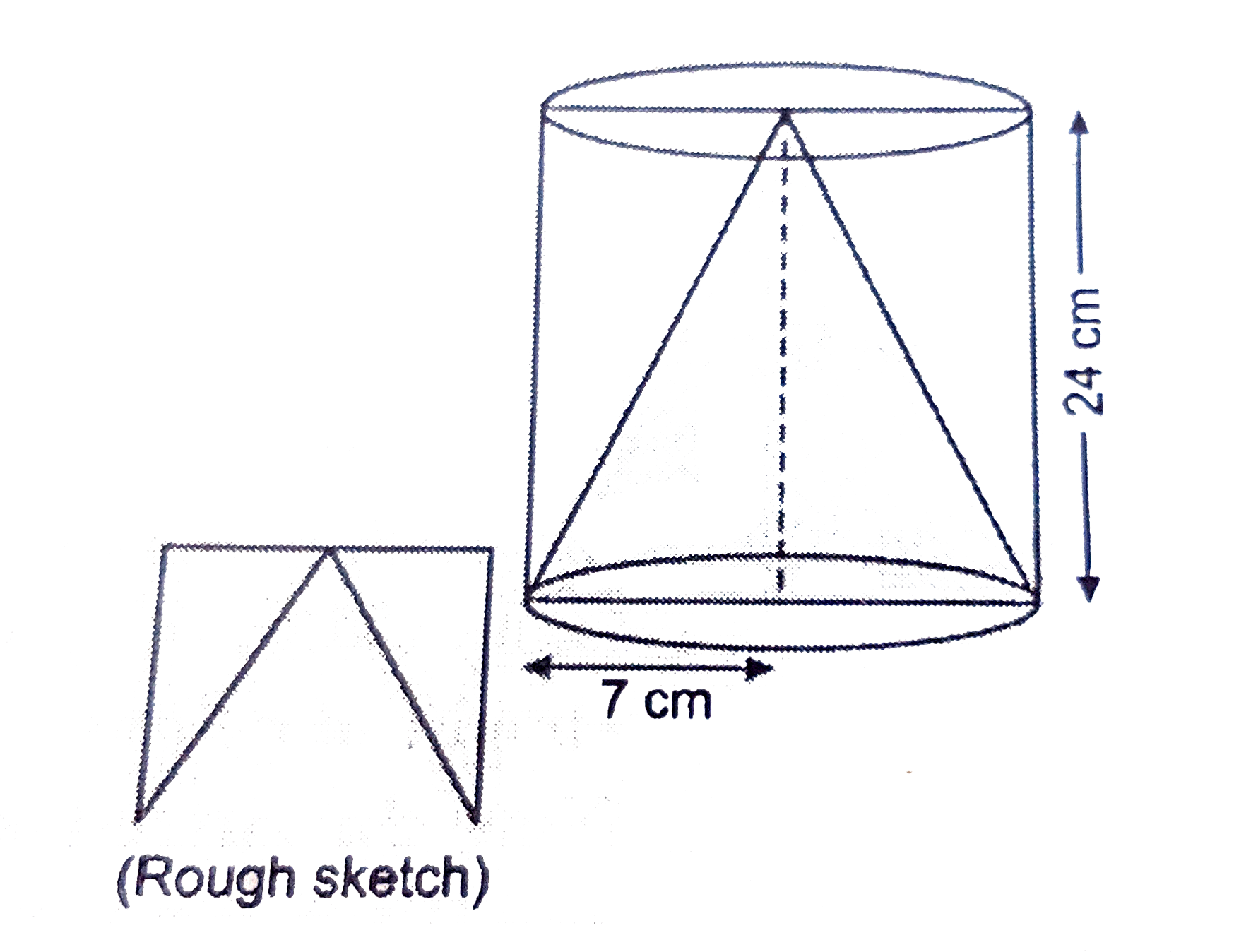
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
From a solid cylinder whose height is 8 cm and radius is 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid.
A $603 c m^{3}$
B $720 c m^{3}$
C $548 c m^{3}$
D $637 c m^{3}$

NAGEEN PRAKASHAN-VOLUME AND SURFACE AREA OF SOLIDS-Revisions Exercise Long Answer Questions

Home
Ask Doubt
Profile