From a solid cylinder of height 36 cm and radius 14 cm a conical cavity of radus 7 cm and height 24 cm is drilled out . Find the volume and the total surface area of the remaining solid.

Video Solution

Text Solution

Verified by Experts

According to the given statement , the figure will be as shown alongside:
Clearly for solid cylinder height (H) =36 cm and radius (R ) =14cm.And for conical cavity height (h)=24 cm radius (c ) =7cm and slant height (l)= $(\sqrt{h^{2} + r^{2}} = (\sqrt{24^{2} + 7^{2}} c m$ =25cm volume of the remaining solid =volume of cylinder -volume of conical cavity
$π R^{2} H - \frac{1}{3} π r^{2} h$
$= \frac{22}{7} \times {(14)}^{2} \times 36 c m^{3} - \frac{1}{3} \times \frac{22}{7} \times {(7)}^{2} \times 24 c m^{3}$
$22176 c m^{3} - 1232 c m^{3}$
$= 20944 c m^{3}$

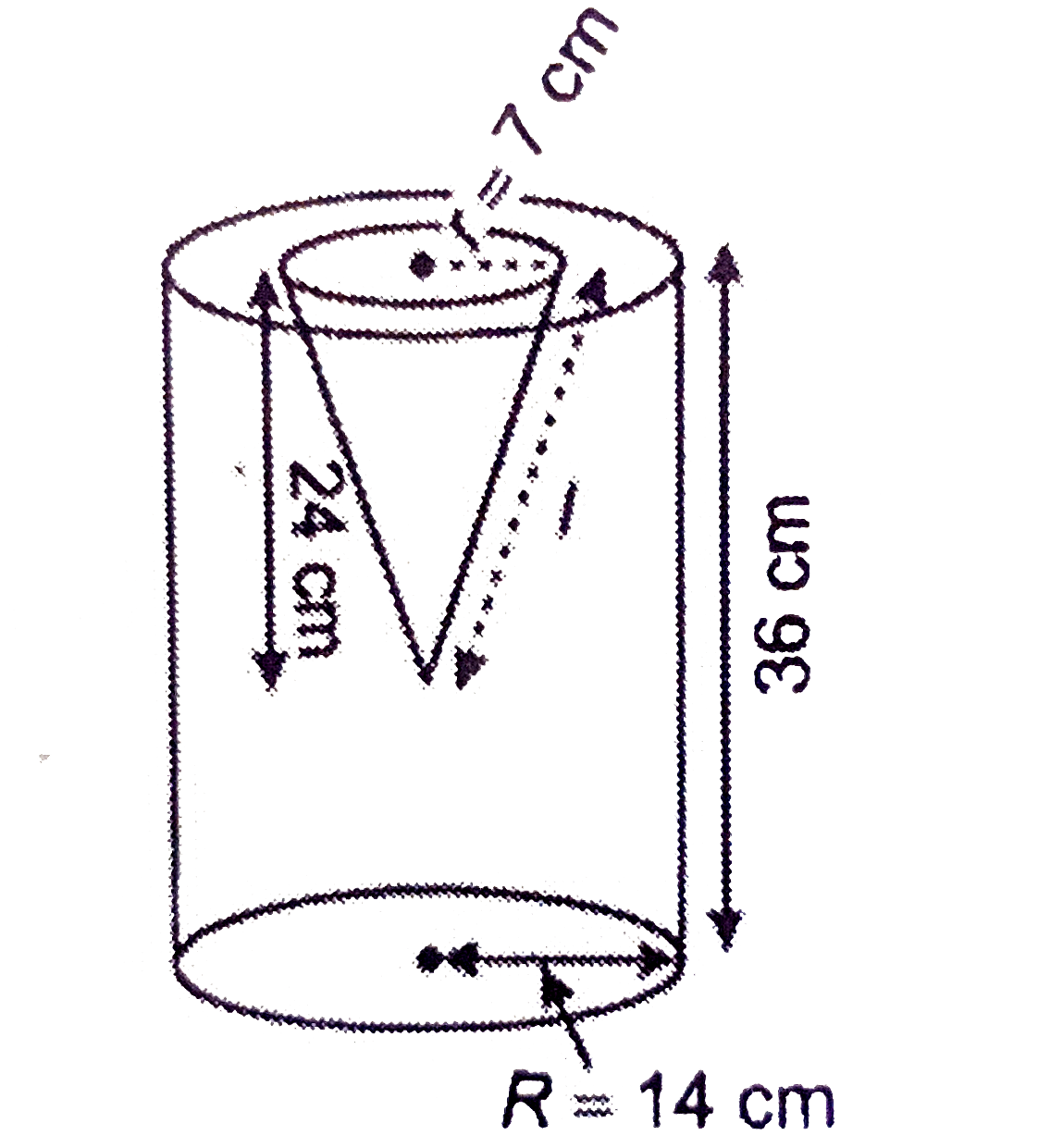
Total surface area of the remaining solid
=Area of the base of the cylinder +cuved surface area of the cylinder +Area of the top ring + curved surface area of the conical cavity
$= π R^{2} + 2 π R H + π (R^{2} - r^{2}) + π r l$
$= \frac{22}{7} [(14^{2} + 2 \times 14 \times 36 + (14^{2} - 7^{2}) + 7 \times 25)] c m^{2}$
$= \frac{22}{7} \times 1526 c m^{2} = 4796 c m^{2}$

Updated on:21/07/2023