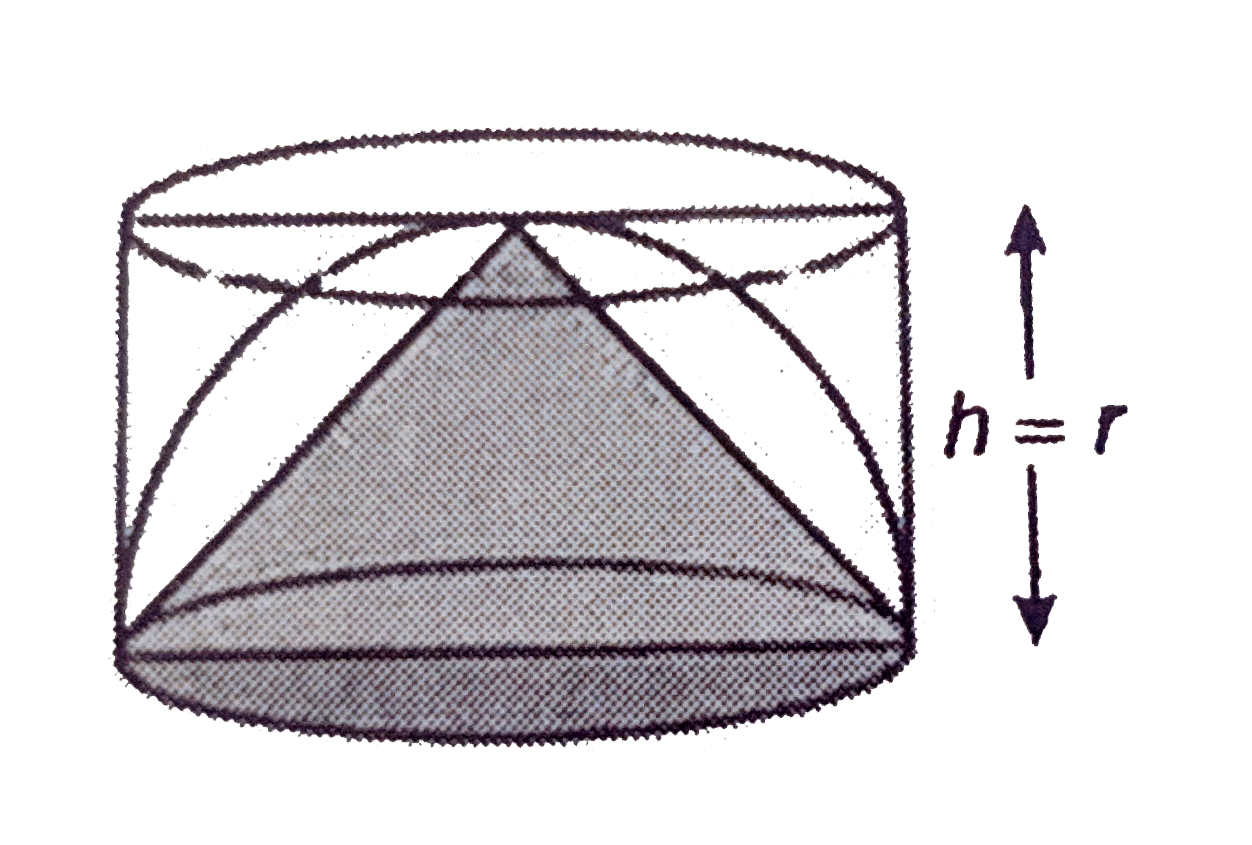
A hemisphere is inscribed in a cylinder and a cone is inscribed in the hemisphere .The vertex of cone lies on the centre of the upper circular part of the cylinder .Show that , $\frac{1}{3} \times$ Volume of cylinder = $\frac{1}{2} \times$ Volume of hemishphere= Volume of cone

Video Solution

Text Solution

Verified by Experts

Let radius of cone = radius of cylinder = radius of hemisphere= r
Height of cone = Height of cylinder = r
Now the volume of cone = $\frac{1}{3} π r^{2} . (r) = \frac{1}{3} π r^{3}$
volume of hemisphere= $\frac{2}{3} π r^{3}$
$\frac{1}{2} \times$ volume of hemisphere= $\frac{1}{3} π r^{3}$
and volume of cylindr = $π r^{2} (r) = π r^{3}$
$\frac{1}{3} \times$ volume of cylinder = $\frac{1}{3} π r^{3}$
From equatioopns (1),(2)and (3)
$\frac{1}{3} \times$ volume of cylinder $= \frac{1}{2} \times$ volume of hemishpere
=volume of cone

Updated on:21/07/2023