The three different face diagonals of a cuboid (rectangular parallelopipd ) have lengths 39,40 and 41 units .Find the length of the main diagonal of the cuboid which joins a pair of opposite corners.

Video Solution

Text Solution

Verified by Experts

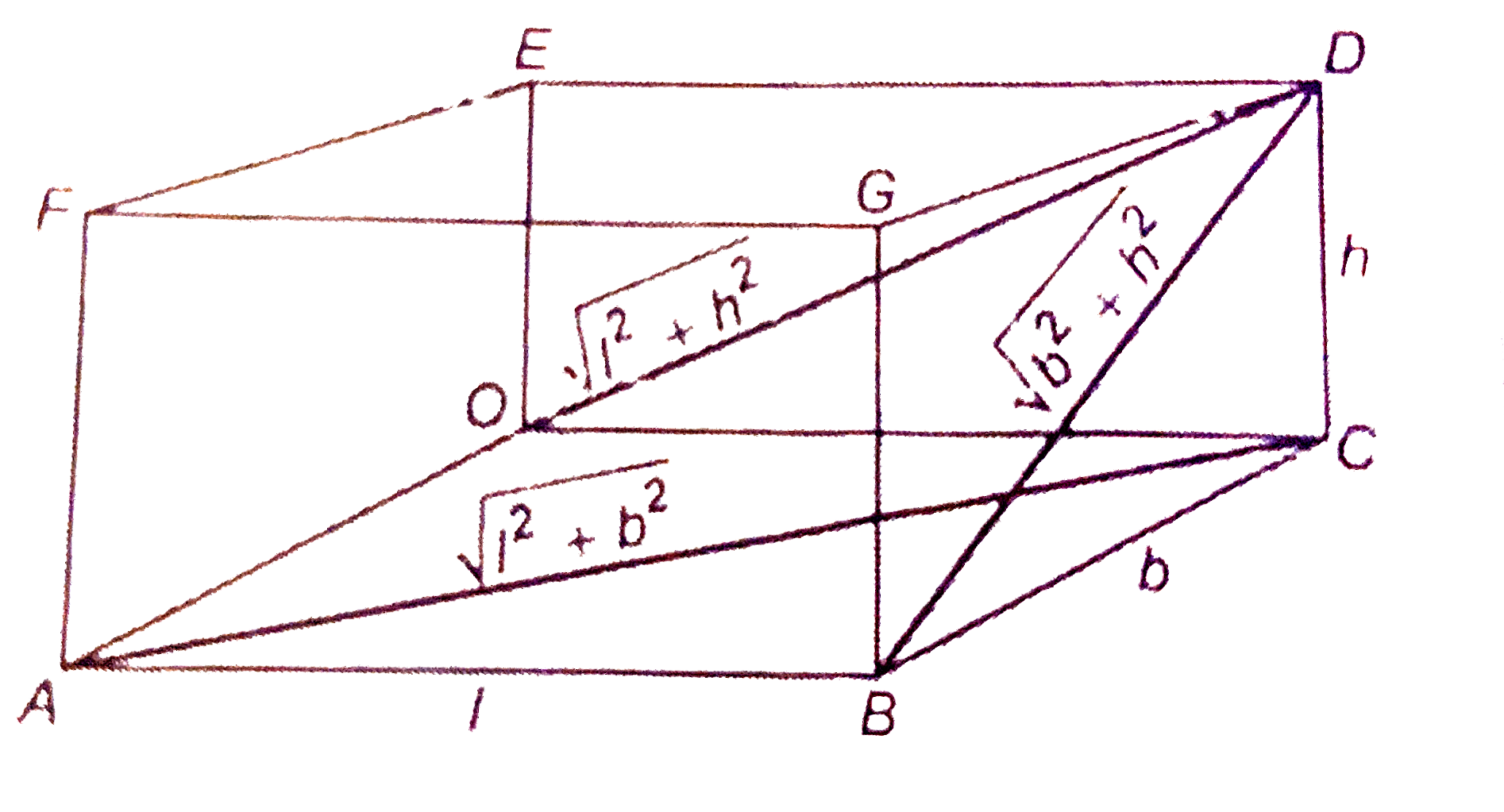
Let l,b,h be the length $(\sqrt{l^{2} + b^{2}}) = 39 \to l$
$(\sqrt{b^{2} + h^{2}}) = 40 \to b^{2} + h^{2} = {(40)}^{2}$ =1600..(2)
$(\sqrt{h^{2} + l^{2}}) = 4 l \to h^{2} + l^{2} = {(41)}^{2} = 168 \dots (3)$
Adding (1),(2)and(3), we get
$2 (l^{2} + b^{2} + h^{2}) = 1521 + 1600 + 1681 = 4802$
$l^{2} + b^{2} + h^{2} = 2401 = (49^{2})$
Length of main diagonal EB= $(\sqrt{l^{2}} + b^{2} + h^{2})) = (\sqrt{49^{2}}) = 49 u n i t s$

Updated on:21/07/2023