Three spheres of radius 'r' are kept inside a cuylinder such that two of the speres are at bottom touching each other and sides of the cylinder while the third sphere is touching the two bottom spheres and the top of the cylinder .Find the volume of the cylinder .
By Pythagoras theorem,
AM=r(√3)
Height of cylinder H=r+r(√3)+r→r(2+(√3))
Radius of cylinder R= 2r
Volume of cylinder =πR2H
=π(2r2).r(2+(√3))=4πr3(2+(√3))
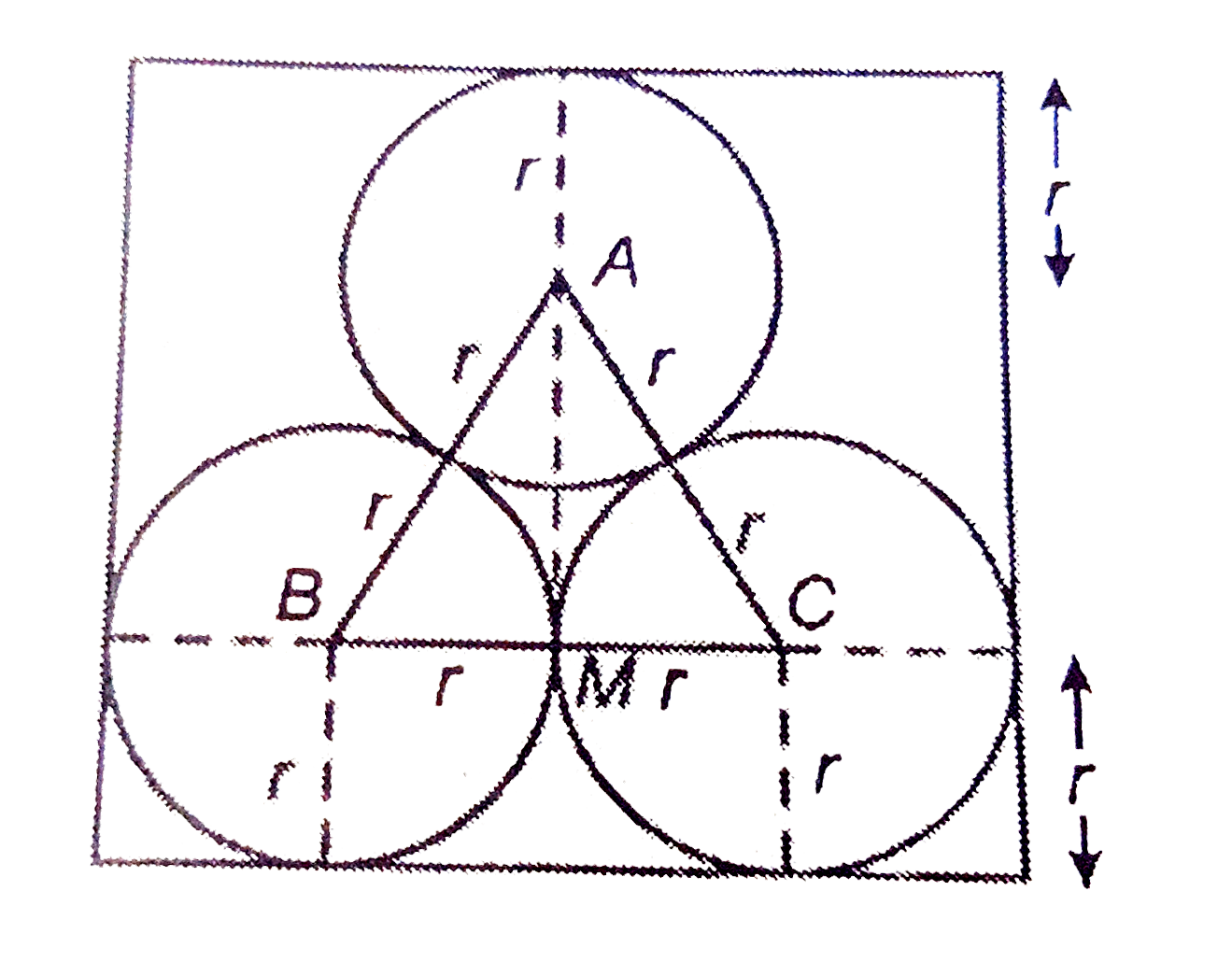
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Problems From NCERT/exemplar10videos
VOLUME AND SURFACE AREA OF SOLIDS
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Exercise68videos
VOLUME AND SURFACE AREA OF SOLIDS
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions4videos
TRIANGLES
Similar Questions
Three spheres of radius 'r ' are kept inside a cylinder such that two of the spheres are at bottom touching each other and sides of the cylinder while the third sphere is touching the two bottom spheres and the top of the cylinder. Then the volume of the cylinder is :
View SolutionAs shown in the adjacent figure, a sphere is placed in a cylinder. It touches the top, bottom and the curved surface of the cylinder. If radius of the base of the cylinder is 'r',
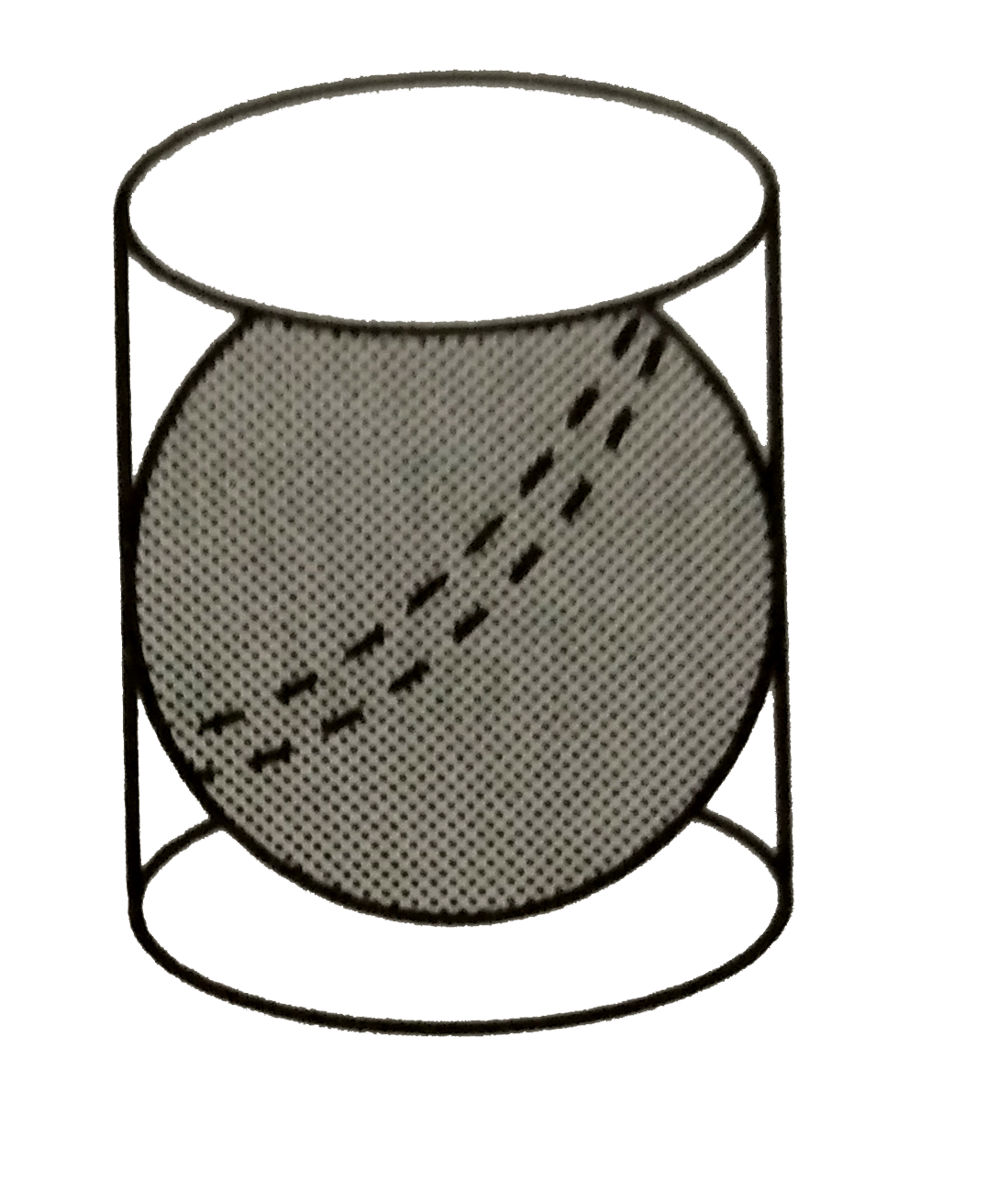
(i) what is ratio of the radii of the sphere and the cylinder?
(ii)what is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
(iii) what is the ratio of the volumes of the cylinder and the sphere?View Solution
Knowledge Check
- Question 1 - Select One
The radius and height of a cylinder are equal. If the radius of the sphere is equal to the height of the cylinder, then the ratio of the rates of increase of the volume of the sphere and the volume of the cylinder, is
A4:3B3:4C4:3πD3π:4 - Question 2 - Select One
When these two spheres are made to touch with each other, then final charge on bigger sphere will be
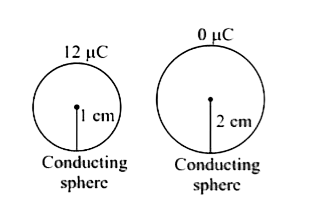 A0μCB12μCC4μCD8μC
A0μCB12μCC4μCD8μC - Question 3 - Select One
The volumes of a sphere and a right circular cylinder having the same radius are equal. The ratio of the diameter of the sphere to the height of the cylinder is
A2πR3B8πR3C43πR3Dnone of these
A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is 4π r3 (b) 83π r3 (c) 2π r3 (d) 8π r3
View SolutionThe radius of a circular cylinder is the same as that of a sphere. Their volumes are equal. The height of the cylinder is ---
View SolutionThe profit earned after selling on article for 1666 is the same as the loss incurred after selling the article for 1252. What is the cost price of the article ?
View SolutionFive spheres are kept in a cone in such a way that each sphere touch each other and also touch the lateral surface of the cone, this is due to increasing radius of the spheres starting from the vertex of the cone . The radius of the smallest sphere is 16 cm.
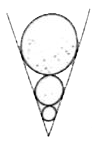
If the radius of the fifth ( i.e, largest ) sphere be 81 cm, then find the radius of the third ( i.e, middlemost) sphere :View SolutionA sphere and a cylinder have equal volume and equal radius. The ratio of the curved surface area of the cylinder to that of the sphere is
View Solution

