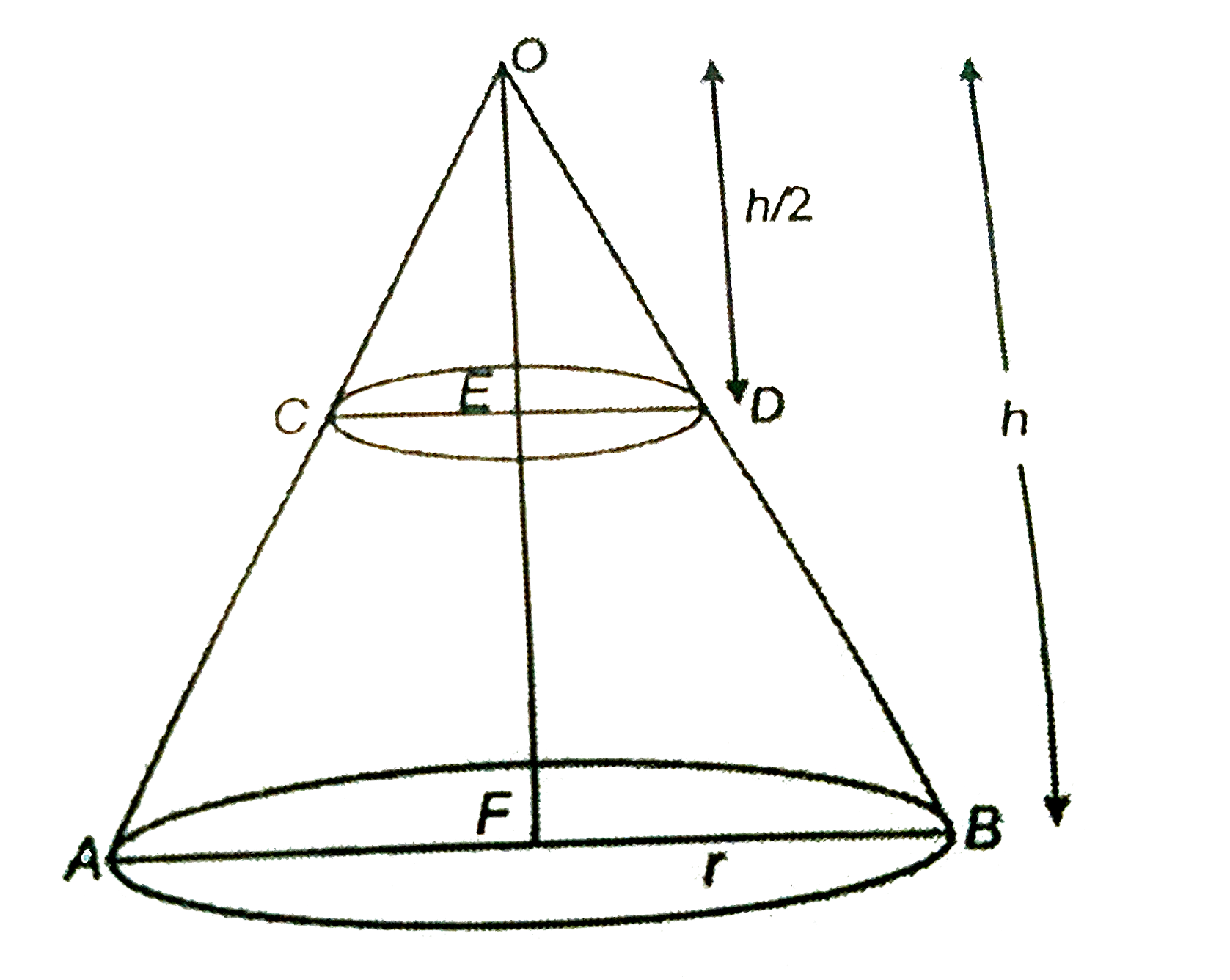
A cone is divided in to two parts by drawing a plane through the mid point of its adis parallel to its base. Compare the volume of two parts.

Video Solution

Text Solution

Verified by Experts

We can solve this using similarity
Let r and h be the radius and height of a cone OAB
Let $O E = \frac{h}{2}$
As OED and OFB are similar
there $\frac{O E}{O F} = \frac{E D}{F B} \frac{h / 2}{h} = \frac{E D}{r}$
$E D = \frac{r}{32}$
Now volume of cone IOCD $= \frac{1}{3} π r^{2} h = \frac{1}{3} \times π \times {(\frac{r}{2})}^{2} \times \frac{h}{2} = \frac{π r^{2} h}{24}$
and volume of cone OAB= $\frac{1}{3} \times π \times r^{2} \times h = \frac{π r^{2} h}{3}$
$∴ \frac{volume of part OCB}{volume of part CDAB} = \frac{π r^{2} h}{\frac{π r^{2} h}{3}} - \frac{π r^{2} h}{24} = \frac{\frac{1}{24}}{\frac{1}{3}} - \frac{1}{24} = \frac{1}{\frac{24}{\frac{8 - 21}{24}}} = \frac{1}{7}$

Updated on:21/07/2023

A cone of radius r сm and height h cm is divided into two parts by drawing a plane through the middle point of its height and parallel to the base. What is the ratio of the volume of the original cone to the volume of the smaller cone?
A $4 : 1$
B $8 : 1$
C $2 : 1$
D $6 : 1$
If a cone is cut into two parts by a horizontal plane passing through the mid-point of its axis, then the ratio of the volumes of the upper part and the given cone is
A1 : 2
B1 : 4
C1 : 6
D1 : 8
If a cone is cut into two parts by a horizontal plane passing through the mid point of its axis , the ratio of the volumes of the upper part and the frustum is :
A $1 : 1$
B $1 : 2$
C $1 : 3$
D $1 : 7$