A circus tent is in the form of a right circular cylinder and right circular cone above it . The diameter and the height of the cylindrical part of the tent are 126 m and 5 m respectively.The totla height of the tent is 21 m. Find the total cost of the tent if the canvas used costsRs 12 per square metre.
The correct Answer is:Rs 178200
To solve the problem, we need to find the total surface area of the circus tent, which consists of a cylindrical part and a conical part, and then calculate the cost based on the area and the cost per square meter.
Step 1: Find the radius and height of the cylindrical part.
- The diameter of the cylindrical part is given as 126 m.
- Therefore, the radius r of the cylindrical part is:
r=diameter2=1262=63m
- The height hc of the cylindrical part is given as 5 m.
Step 2: Find the height of the conical part.
- The total height of the tent is given as 21 m.
- The height hcone of the conical part can be calculated as:
hcone=Total height−Height of cylindrical part=21−5=16m
Step 3: Calculate the surface area of the cylindrical part.
- The formula for the lateral surface area Ac of a cylinder is:
Ac=2πrhc
- Substituting the values:
Ac=2×π×63×5
Ac=630πm2
Step 4: Calculate the slant height of the conical part.
- The slant height l of the cone can be found using the Pythagorean theorem:
l=√r2+h2cone=√632+162
l=√3969+256=√4225=65m
Step 5: Calculate the surface area of the conical part.
- The formula for the lateral surface area Acone of a cone is:
Acone=πrl
- Substituting the values:
Acone=π×63×65
Acone=4095πm2
Step 6: Calculate the total surface area of the tent.
- The total surface area Atotal is the sum of the surface areas of the cylindrical and conical parts:
Atotal=Ac+Acone=630π+4095π=4725πm2
Step 7: Calculate the cost of the canvas.
- The cost per square meter is given as Rs 12.
- Therefore, the total cost C is:
C=Atotal×cost per square meter=4725π×12
- Approximating π as 3.14:
C≈4725×3.14×12
C≈4725×37.68≈177,078Rs
Final Answer:
The total cost of the tent is approximately Rs 177,078.
---
- The diameter of the cylindrical part is given as 126 m.
- Therefore, the radius r of the cylindrical part is:
r=diameter2=1262=63m
- The height hc of the cylindrical part is given as 5 m.
- The total height of the tent is given as 21 m.
- The height hcone of the conical part can be calculated as:
hcone=Total height−Height of cylindrical part=21−5=16m
- The formula for the lateral surface area Ac of a cylinder is:
Ac=2πrhc
- Substituting the values:
Ac=2×π×63×5
Ac=630πm2
- The slant height l of the cone can be found using the Pythagorean theorem:
l=√r2+h2cone=√632+162
l=√3969+256=√4225=65m
- The formula for the lateral surface area Acone of a cone is:
Acone=πrl
- Substituting the values:
Acone=π×63×65
Acone=4095πm2
- The total surface area Atotal is the sum of the surface areas of the cylindrical and conical parts:
Atotal=Ac+Acone=630π+4095π=4725πm2
- The cost per square meter is given as Rs 12.
- Therefore, the total cost C is:
C=Atotal×cost per square meter=4725π×12
- Approximating π as 3.14:
C≈4725×3.14×12
C≈4725×37.68≈177,078Rs
The total cost of the tent is approximately Rs 177,078.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Very Short Answer Questions10videos
VOLUME AND SURFACE AREA OF SOLIDS
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Short Answer Questions10videos
VOLUME AND SURFACE AREA OF SOLIDS
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Problems From NCERT/exemplar10videos
VOLUME AND SURFACE AREA OF SOLIDS
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions4videos
TRIANGLES
Similar Questions
For the next three (03) items that follow :
A tent of a circus is made of canvas and is in the form of right circular cylinder and right circular cone above it. The height and diameter of the cylindrical part of the tent are 5 m and 126 m respectively. The total height of the tent is 21 m.
What is the slant height of the cone ?View SolutionA tent of a circus is made of canvas and is in the form of right circular cylinder and right circular cone above it. The height and diameter of the cylindrical part of the tent are 5 m and 126 m respectively. The total height of the tent is 21 m.
What is the curved surface area of the cylinder ?View Solution
Knowledge Check
- Question 1 - Select One
The diameter and the slant height of a conical tent are 16 m and 5 .6 m. respectively. What length of cloth having width 4 m is needed to make the tent?
A35.2 mB32.5 mC32 mD35 m
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is 16 m above the ground. Find the area of canvas required for the tent.
View SolutionA tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24m. The height of the cylindrical portion is 11m while the vertex of the cone is 16m above the ground. Find the area of the canvas required for the tent.
View SolutionA tent is in the form of a right circular cylinder surmounted by a cone. The diameter of the cylinder is 24m. The height of the cylindrical portion is 11m, while the vertex of the cone is 16m above the ground.Find the area of the convas required for tent:
View SolutionThe base radius and height of a conical tent are 8 m and 15 m respectively. Find the area of the cloth used in this tent.
View SolutionThe lower part of a circus tent is a right circualr cylinder and its upper part is right circular cone. The diameter of the base of the tent is 56 m and height of the cylindrical part is 15 m. The total height of the tent is 60 m. How many square metres of canvas is required for the tent? Find the volume of the air space in tent (π=227)
View SolutionA tent has been constructed which is in the form of a right circular cylinder surmounted by a right circular cone whose axis coincides with the axis of the cylinder. If the radius of the base of the cylinder is 50 m, the height of the cylinder is 10 m and the total height of the tent is 15 m, then what is the capacity of the tent in cubic metres ?
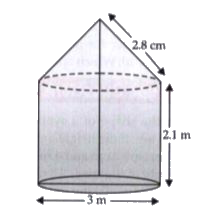
View SolutionIn figure , a tent is in the shape of a cylinder surmounted by a conical top of same diameter . If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m , find the cost of convas needed to make the tent if the canvas is available at the rate of rupees 500/sq.metre .( use π=227)
 View Solution
View Solution

