For the equilibrium A⇔B , the variation of the rate of the forward (a) and reverse (b) reaction with time is given by :
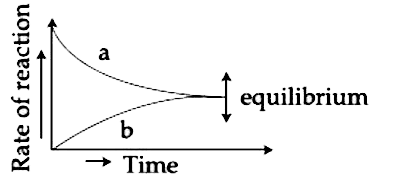
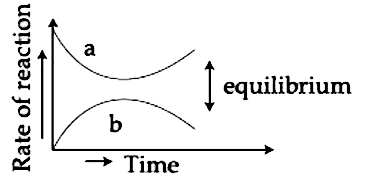

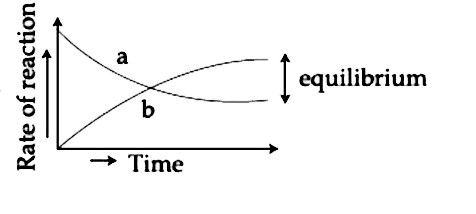
The correct Answer is:A
To solve the problem regarding the equilibrium of the reaction A⇌B and the variation of the rates of the forward and reverse reactions over time, we can follow these steps:
Step 1: Understand the Concept of Equilibrium
At equilibrium, the rate of the forward reaction (formation of B from A) is equal to the rate of the reverse reaction (formation of A from B). This means that the concentrations of A and B remain constant over time.
Hint: Remember that at equilibrium, the rates of the forward and reverse reactions are equal.
Step 2: Analyze the Rate Expressions
Let’s denote the rate of the forward reaction as rf and the rate of the reverse reaction as rb. At equilibrium, we can express this as:
rf=kf(A)
rb=kb(B)
Where kf and kb are the rate constants for the forward and reverse reactions, respectively.
Hint: Write down the rate expressions for both the forward and reverse reactions.
Step 3: Set Up the Equilibrium Condition
At equilibrium, we have:
kf(A)=kb(B)
This equation indicates that the concentrations of A and B are related through their respective rate constants.
Hint: Use the equality of the rates to set up an equation involving concentrations.
Step 4: Determine the Changes Over Time
Initially, as the reaction proceeds, the concentration of A will decrease while the concentration of B will increase. Over time, the rates of the reactions will change until they reach equilibrium.
Hint: Consider how the concentrations of A and B change over time until they stabilize.
Step 5: Conclusion
At equilibrium, since the rates are equal, we can conclude that:
At equilibrium, rf=rb
This means that the system has reached a state where the concentrations of A and B do not change, and the forward and reverse reactions continue to occur at the same rate.
Hint: Remember that equilibrium is a dynamic state where reactions continue to occur, but there is no net change in concentrations.
Final Answer
The correct option regarding the equilibrium of the reaction A⇌B is that the rate of the forward reaction equals the rate of the reverse reaction at equilibrium.
---
At equilibrium, the rate of the forward reaction (formation of B from A) is equal to the rate of the reverse reaction (formation of A from B). This means that the concentrations of A and B remain constant over time.
Let’s denote the rate of the forward reaction as rf and the rate of the reverse reaction as rb. At equilibrium, we can express this as:
rf=kf(A)
rb=kb(B)
Where kf and kb are the rate constants for the forward and reverse reactions, respectively.
At equilibrium, we have:
kf(A)=kb(B)
This equation indicates that the concentrations of A and B are related through their respective rate constants.
Initially, as the reaction proceeds, the concentration of A will decrease while the concentration of B will increase. Over time, the rates of the reactions will change until they reach equilibrium.
At equilibrium, since the rates are equal, we can conclude that:
At equilibrium, rf=rb
This means that the system has reached a state where the concentrations of A and B do not change, and the forward and reverse reactions continue to occur at the same rate.
The correct option regarding the equilibrium of the reaction A⇌B is that the rate of the forward reaction equals the rate of the reverse reaction at equilibrium.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The rate of the backward reaction in a reversible reaction
ApositiveBnegativeCEither (a) or (b)DNone of the above - Question 2 - Select One
If a system is at equilibrium, the rate of forward to the reverse reaction is :
AlessBequalChighDat equilibrium - Question 3 - Select One
If a system is at equilibrium, the rate of forward to the reverse reaction is :
AlessBequalChighDat equilibrium
For the equilibrium, A(g)⇔B(g),ΔH is −40kJ/mol, if the ratio of the activation energies of the forward (Ef) and reverse (Eb) reactions is 2/3, then
View SolutionA reaction having equal energies of activation for forward and reverse reactions has
View SolutionA reaction having equal energies of activation for forward and reverse reactions has
View SolutionFor the reversible reaction,A+B⇔C, the specific reaction rates for forward and reverse reactions are 1.25×103and2.75×104 respectively. The equilibrium constant for the reaction is:
View SolutionA reaction having equal energies of activation for forward and reverse reactions has
View Solution

