Find out the angle made by (ˆi+ˆj) vector from X and Y axes respectively.
a=√a2x+a2y=√12+12=√2
cosα=axa=1√2∴α=45∘
cosβ=aya=1√2∴β=45∘ˆi+ˆj is at bisector of X and Y axes.
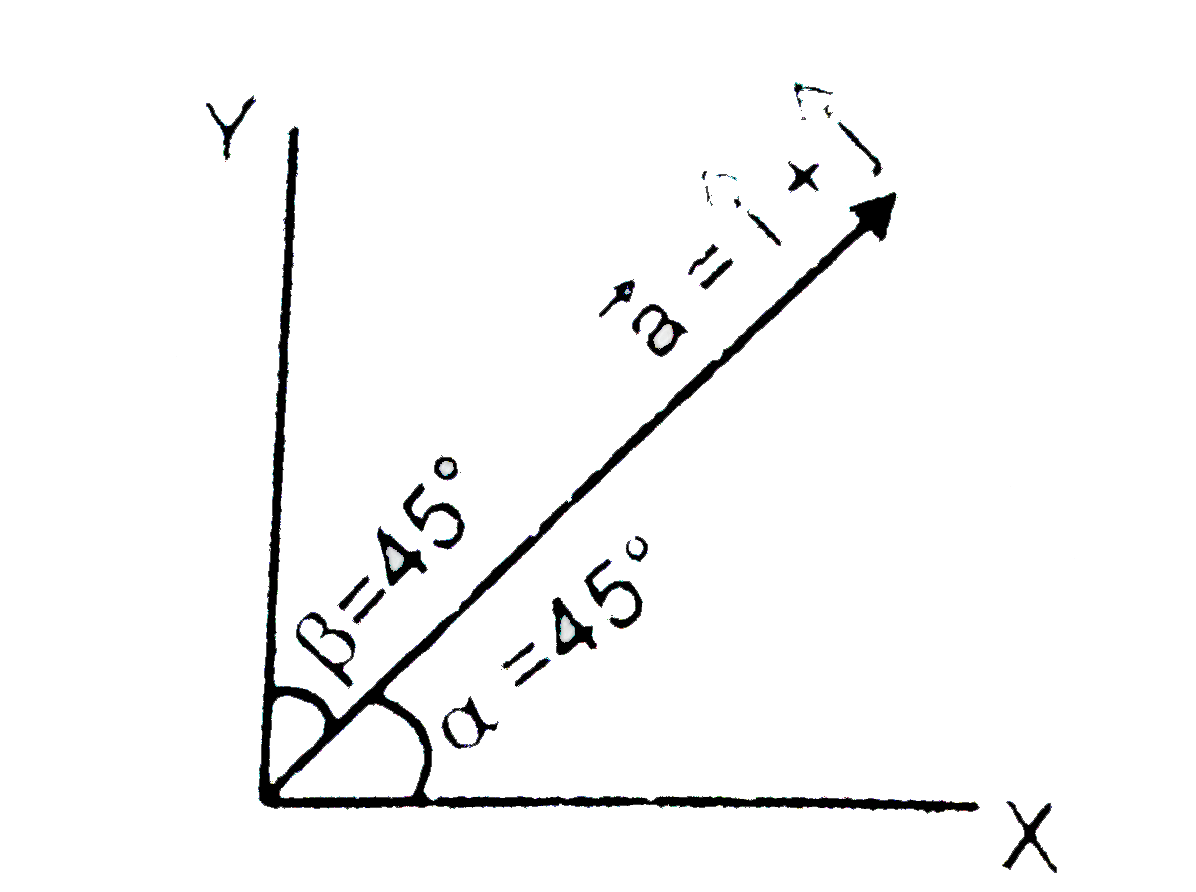
Topper's Solved these Questions
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-1
128 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-2
80 Videos
- AIIMS 2019BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
Knowledge Check
The angle made by the vector →A=ˆi+ˆj with x-axis is
A90∘B45∘C22.5∘D30∘The angle made by the vector →A=2ˆi+3ˆj with Y-axis is
Atan−1(32)Btan−1(23)Csin−1(23)Dcos−1(32)
Find out the angle made by →A=ˆi+ˆj+ˆk vector from X, Y and Z axes respectively.
View SolutionIf ˆi,ˆj and ˆk represent unit vectors along the x,y and z-axes respectively, then the angle θ between the vectors (ˆi+ˆj+ˆk) and (ˆi+ˆj) is equal to :
View SolutionIf ˆi,ˆjandˆk represent unit vectors along the x, y and z-axes respectively, then the angle θ between the vectors (ˆi+ˆj+ˆk)and(ˆi+ˆj) is equal to :
View SolutionTwo unit vectors ˆi and ˆj are directed along x-axis and y-axis respectively. What is the magnitude and direction of the vectors ˆi+ˆjandˆi−ˆj?
View SolutionFind the angles made by →a=3ˆi−6ˆj+2ˆk with the coordinate axes (standard basis vectors).
Any vector in 3-D can be written as
View SolutionFind the angle made by the following vector with the coordinates axes:
(ˆi+ˆj+ˆk)
(ˆj−ˆk)
(ˆi−4ˆj+8ˆk)
View Solution
