Given that P=Q=R. if $\to P + \to Q = \to R$ then the angle between $\to P & \to R$ is $θ_{1}$ then the angle between $\to P & \to R$ is $θ_{2}$ . What is the relation between $θ_{1}$ and $θ_{2}$ .

A

$θ_{1} = θ_{2}$

B

$θ_{1} = \frac{θ_{1}}{2}$

C

$θ_{1} = 2 θ_{2}$

D

none of the above

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

P=Q=R and $\to P + \to Q = \to R$
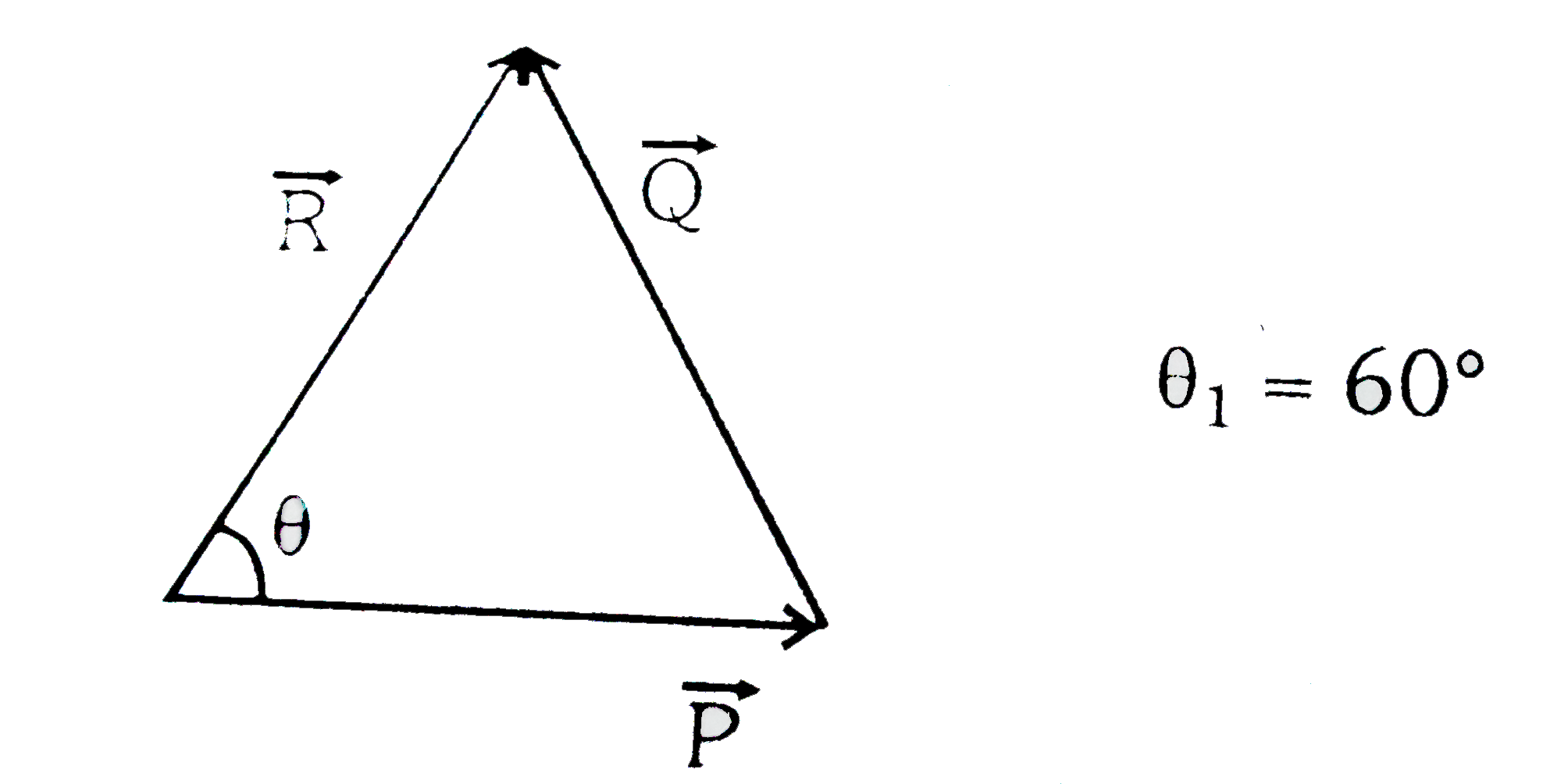$θ_{1} = 60^{\circ}$
If $P = Q = R$ and $\to P + \to Q + \to R = 0$
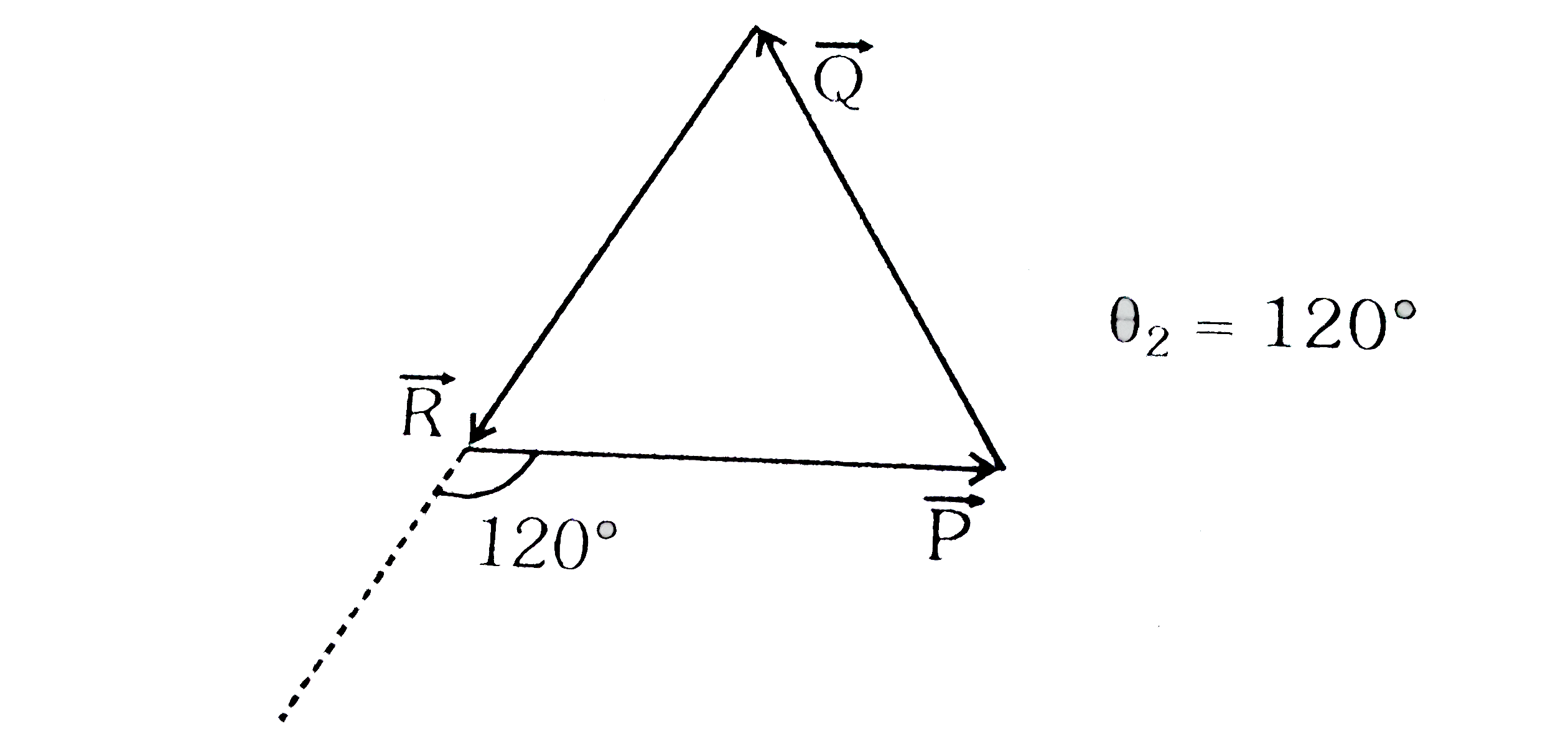$θ_{2} = 120^{\circ}$

|

Updated on:21/07/2023

Class 12 PHYSICS BASIC MATHS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Given that $P = Q = R$ . If $\to P + \to Q = \to R$ then the angle between $\to P & \to R$ is $θ_{1}$ . If $\to P + \to Q + \to R = \to 0$ then the angle between $\to P & \to R$ is $θ_{2}$ . What is the relation between $θ_{1} and θ_{2}$ ?
A $θ_{1} = θ_{2}$
B $θ_{1} = \frac{θ_{2}}{2}$
C $θ_{1} = 2 θ_{2}$
DNone of the above
Question 2 - Select One
If $\to P . \to Q = P Q$ then angle between $\to P$ and $\to Q$ is
A $0^{\circ}$
B $30^{\circ}$
C $45^{\circ}$
D $60^{\circ}$
Question 3 - Select One
If $∣ ∣ \to P + \to Q ∣ ∣ = ∣ ∣ \to P - \to Q ∣ ∣$ the angle between $\to P and \to Q$ is
A $0^{\circ}$
B $90^{\circ}$
C $180^{\circ}$
D $45^{\circ}$

ALLEN-BASIC MATHS-EXERCISE-1

Home
Ask Doubt
Profile