Velocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
To solve the problem of calculating the displacement of a particle whose velocity varies with time as v=4t, we can follow these steps:
Step 1: Understand the relationship between velocity and displacement
The velocity v of a particle is defined as the rate of change of displacement s with respect to time t:
v=dsdt
Step 2: Substitute the given velocity function
We are given that v=4t. Therefore, we can write:
dsdt=4t
Step 3: Rearrange the equation to separate variables
We can rearrange the equation to separate the variables s and t:
ds=4tdt
Step 4: Integrate both sides
Now we integrate both sides. The left side integrates with respect to s and the right side with respect to t:
∫ds=∫4tdt
This gives us:
s=2t2+C
where C is the constant of integration.
Step 5: Determine the constant of integration
To find the constant C, we need to know the initial condition. Let's assume the displacement s=0 at t=0:
0=2(0)2+C⟹C=0
Thus, the equation for displacement simplifies to:
s=2t2
Step 6: Calculate displacement between t=2 and t=4
Now we can calculate the displacement at t=2 seconds and t=4 seconds:
1. For t=4:
s(4)=2(42)=2×16=32meters
2. For t=2:
s(2)=2(22)=2×4=8meters
Step 7: Find the displacement between the two times
The displacement between t=2 seconds and t=4 seconds is:
Δs=s(4)−s(2)=32−8=24meters
Final Answer
The displacement of the particle between t=2 seconds and t=4 seconds is 24 meters.
---
The velocity v of a particle is defined as the rate of change of displacement s with respect to time t:
v=dsdt
We are given that v=4t. Therefore, we can write:
dsdt=4t
We can rearrange the equation to separate the variables s and t:
ds=4tdt
Now we integrate both sides. The left side integrates with respect to s and the right side with respect to t:
∫ds=∫4tdt
This gives us:
s=2t2+C
where C is the constant of integration.
To find the constant C, we need to know the initial condition. Let's assume the displacement s=0 at t=0:
0=2(0)2+C⟹C=0
Thus, the equation for displacement simplifies to:
s=2t2
Now we can calculate the displacement at t=2 seconds and t=4 seconds:
1. For t=4:
s(4)=2(42)=2×16=32meters
2. For t=2:
s(2)=2(22)=2×4=8meters
The displacement between t=2 seconds and t=4 seconds is:
Δs=s(4)−s(2)=32−8=24meters
The displacement of the particle between t=2 seconds and t=4 seconds is 24 meters.
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-1
99 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-2
170 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
48 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
(a) If s=2t3+3t2+2t+8 then find time at which acceleration is zero.
(b) Velocity of a particle (starting at t =0) varies with time as v= 4t. Calculate the displacement of part between t = 2 to t = 4 s
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View Solution
Knowledge Check
If the displacement of a particle varies with time as √x=t+3
Avelocity of the particle is inversely proportional to tBvelocity of particle varies linearly with tCvelocity of particle is proportional to √tDinitial velocity of the particle is zeroIf displacements of a particle varies with time t as s=1t2 , then.
AThe particle is moving with constant velocityBThe particle is moving with variable acceleration of decreasing orderCThe particle is moving with constant retardationDThe particle has constant speed but variable velocityIn the above question, the displacement of particle at t = 1 sec and x = 4 cm is:
A4 cmB2cmC1cmDZero
The acceleration of a particle varies with time as shown in .
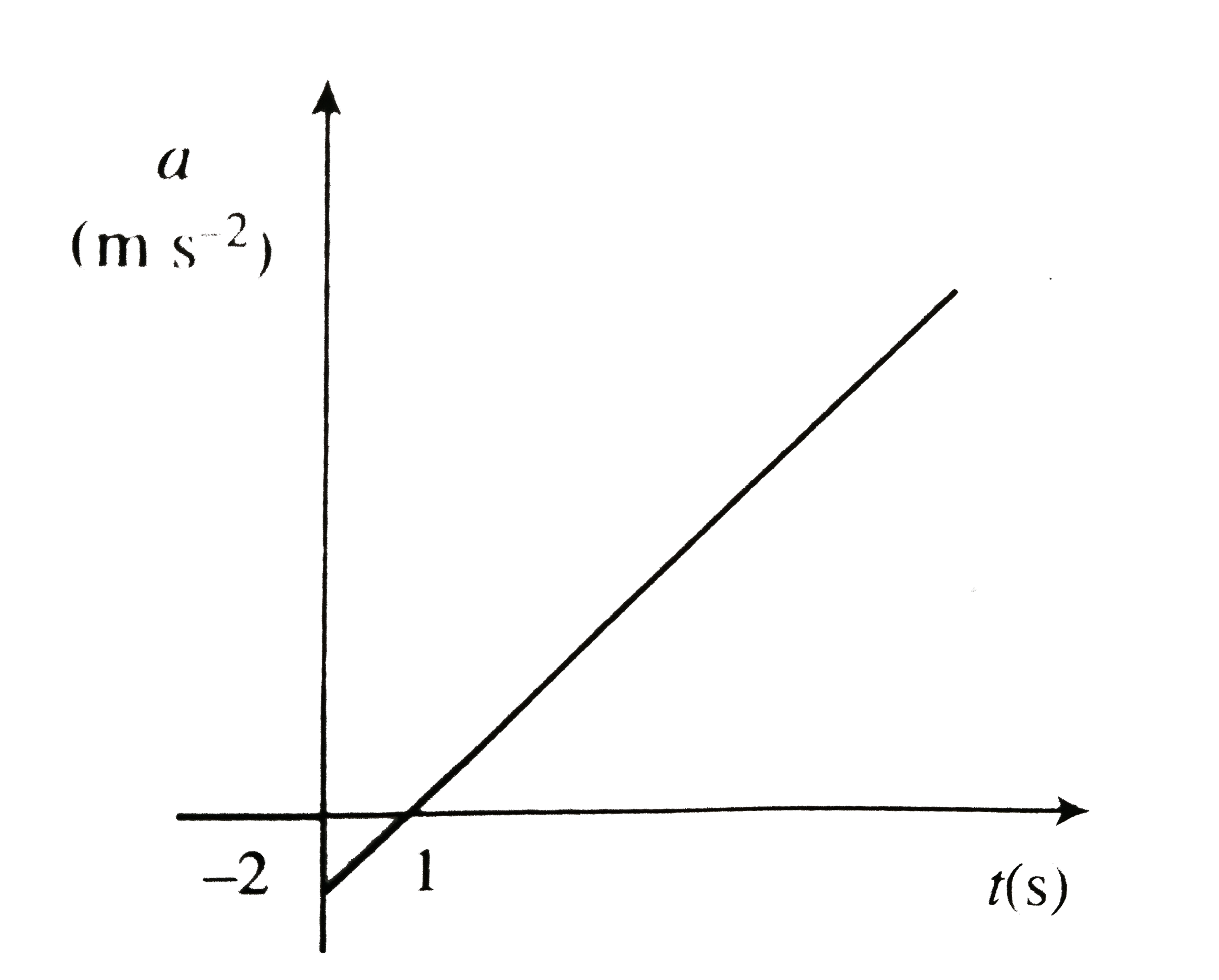 .
.
a. Find an expression for velocityinterms of t. Assume that v=0 at t=0
b. Calculate the displacement of the paarticle in the time interval from t=2s s.
View SolutionVelocity of a particle at any time t is v=(2ˆi+2tˆj)m/s. Find acceleration and displacement of particle at t=1s. Can we apply v=u+at or not?
View SolutionThe position of a particle varies with function of time as y=(4sint+3cost)m. Then the maximum displacement of the particle from origin will be
View Solutionthe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
View SolutionA particle is moving with velocity v=4t3+3t2−1m/s.
The displacement of particle in time t=1s to t=2s will be
View Solution
