A train accelerates from rest at a constant rate a for distance x1 and time t91). After that is retards at constant rate β for distance x2 and time t2 and comes to the rest. Which of the following relation is correct:-
x1x2=αβ=t1t2
x1t2=βα=t1t2
x1x2=αβ=t2t1
x1x2=βα=t2t1
The correct Answer is:B
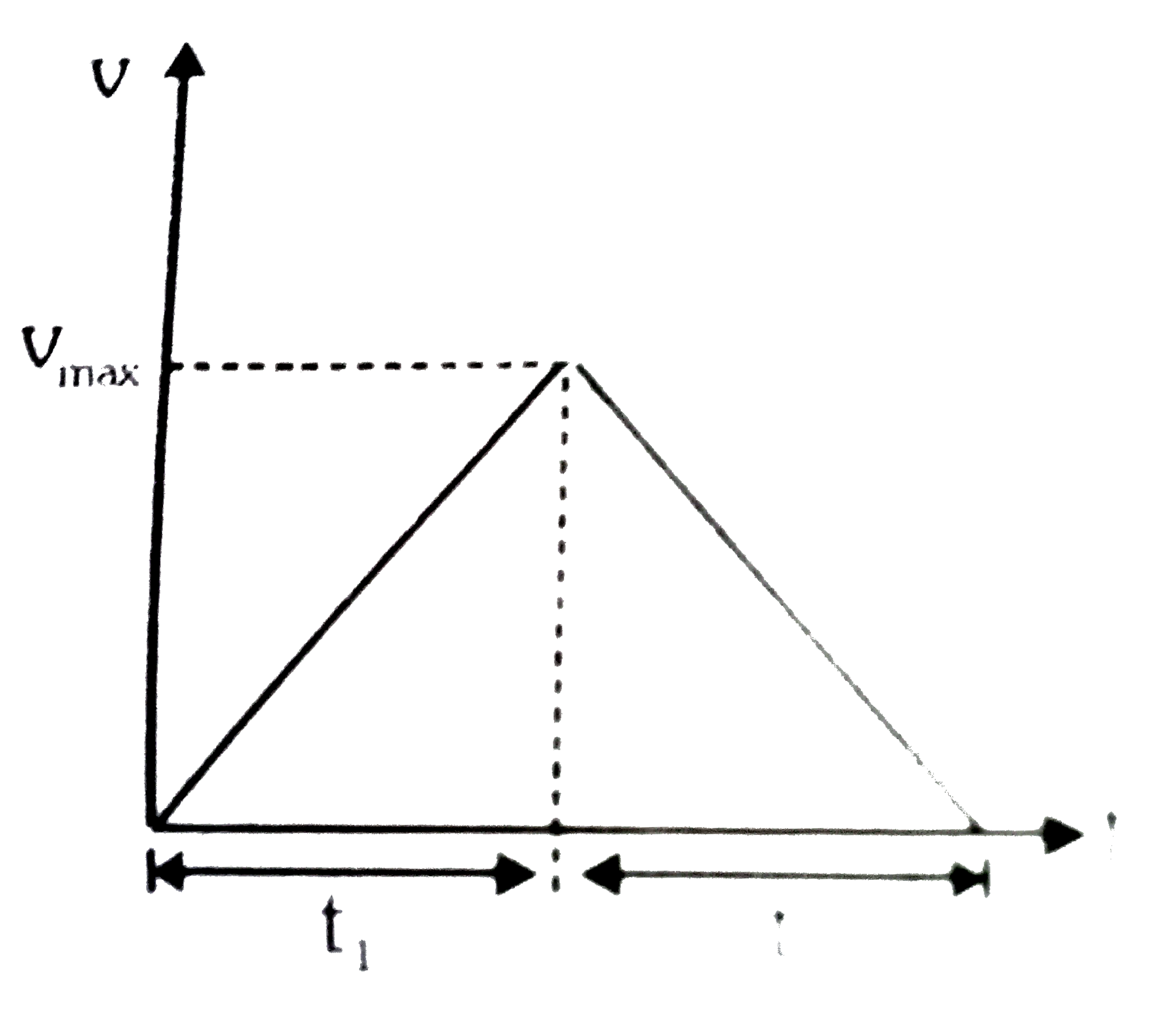
tanα=slope=vmaxt1⇒α=tan−1(vmaxt1)
tanβ=slope==vmaxt2⇒β=tan−1(Vmaxt2)
∴βα=vmaxt2vmaxt1=t1t2
Area of (v-t) graph= displacement
During acceleration graph x1=12×t1vmax ....(1)
During retarding graph x2=12×t2vmax....(2)
Now x1x2=t1t2 so x1x2=t1t2=βα
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-341videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE28videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-199videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)48videos
KINEMATICS-2D
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
Similar Questions
An elevator accelerates from rest at a constant rate α for time interval t1 and travels a distance S1 It them retards at a constant rate β for time interval t2 and finally comes to rest after travelling a distance S2 during its retardation Show that:
S1S2=t1t2=βα.View SolutionA train accelerates from at the constant rate b for time t2 at a constant rate a and then it retards at the comes to rest. Find the ratiot1//t2.
View Solution
Knowledge Check
- Question 1 - Select One
A train accelerates from rest at a constant rate for distance \X1 and time .\t1 After that retards to rst at constant rate for distance X2 and time t2 . Then, it is found that
AX1X2=αβ=t1t2BX1X2=αβ=t2t1CX1X2=βα=t1t2DX1X2=βα=t2t1 - Question 2 - Select One or More
A train moves from rest with acceleration α and in time t1 covers a distance x. It then decelerates rest at constant retardation β for distance y in time t2. Then
Axy=βαBβα=t1t2Cx=yDxy=βt1αt2 - Question 3 - Select One
A scooter accelerates from rest for time t1 at constant rate a1 and then retards at constant rate a2 for time t2 and comes to rest. The correct value of t1t2 will be :-
Aa1+a2a2Ba2a1Ca1a2Da1+a2a1
A car, starting from rest, has a constant acceleration for a time interval t1 during which it covers a distance In the next time interval the car has a constant retardation and comes to rest after covering a distance in time Which of the following relations is correct?
View SolutionA car accelerates from rest at constant rate of 2ms−2 for some time. Then it retards at a constant rate of 4ms−2 and comes to rest. It remains in motion for 3 seconds
View SolutionA car accelerates from rest at constant rate of 2ms−2 for some time. Immediately after this, it retards at a constant rate of 4ms−2 and comes to rest. The total time for which it remains in motion is 3 s. Taking the moment of start of motion as t = 0, answer the following questions.
If the time of acceleration is t1, then the speed of the car at t=t1 isView SolutionA car accelerates from rest at constant rate of 2ms−2 for some time. Immediately after this, it retards at a constant rate of 4ms−2 and comes to rest. The total time for which it remains in motion is 3 s. Taking the moment of start of motion as t = 0, answer the following questions.
Let t be a time instant greater than t1 but less than 3 s. The velocity at this time instant isView SolutionA car accelerates from rest at constant rate of 2ms−2 for some time. Immediately after this, it retards at a constant rate of 4ms−2 and comes to rest. The total time for which it remains in motion is 3 s. Taking the moment of start of motion as t = 0, answer the following questions.
What is the distance travelled by it during the time of decreasing speed ?View Solution

