A river is flowing at the rate of 6 km/hr. A swimmer swims across with a velocity of 9 km/hr w.r.t. water. The resultant velocity of the man will be in (km/hr):-
√117
√340
√17
3√40
The correct Answer is:A
To solve the problem of finding the resultant velocity of a swimmer swimming across a river, we can follow these steps:
1. Identify the velocities:
- The velocity of the river (Vr) is 6 km/hr.
- The velocity of the swimmer with respect to the water (Vs) is 9 km/hr.
2. Set up the coordinate system:
- Assume the river flows along the x-axis (horizontal direction).
- The swimmer swims across the river, which we can assume to be along the y-axis (vertical direction).
3. Represent the velocities as vectors:
- The velocity of the swimmer can be represented as a vector: Vs=9^j km/hr (where ^j is the unit vector in the y-direction).
- The velocity of the river can be represented as a vector: Vr=6^i km/hr (where ^i is the unit vector in the x-direction).
4. Calculate the resultant velocity:
- The resultant velocity (Vresultant) of the swimmer can be found by adding the two vectors:
Vresultant=Vs+Vr=9^j+6^i
5. Find the magnitude of the resultant velocity:
- To find the magnitude of the resultant velocity, we use the Pythagorean theorem:
|Vresultant|=√(Vr)2+(Vs)2=√(6)2+(9)2
- Calculate the squares:
=√36+81=√117
6. Calculate the numerical value:
- The numerical value of √117 can be approximated:
√117≈10.82 km/hr
Final Answer:
The resultant velocity of the swimmer is approximately 10.82 km/hr.
---
- The velocity of the river (Vr) is 6 km/hr.
- The velocity of the swimmer with respect to the water (Vs) is 9 km/hr.
- Assume the river flows along the x-axis (horizontal direction).
- The swimmer swims across the river, which we can assume to be along the y-axis (vertical direction).
- The velocity of the swimmer can be represented as a vector: Vs=9^j km/hr (where ^j is the unit vector in the y-direction).
- The velocity of the river can be represented as a vector: Vr=6^i km/hr (where ^i is the unit vector in the x-direction).
- The resultant velocity (Vresultant) of the swimmer can be found by adding the two vectors:
Vresultant=Vs+Vr=9^j+6^i
- To find the magnitude of the resultant velocity, we use the Pythagorean theorem:
|Vresultant|=√(Vr)2+(Vs)2=√(6)2+(9)2
- Calculate the squares:
=√36+81=√117
- The numerical value of √117 can be approximated:
√117≈10.82 km/hr
The resultant velocity of the swimmer is approximately 10.82 km/hr.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-341videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE28videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-199videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)48videos
KINEMATICS-2D
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
Similar Questions
(A): Rain is falling vertically downwards with velocity 6 km/hr. A man walks with a velocity of 8 km/hr. Relative velocity of rain w.r.t. the man is 10km/hr.
(R): Relative velocity is the ratio of two velocities.View SolutionA river flows at the rate of 3km/hr and a person can row a boat at a speed of 5km/hr in still water.If the difference between the times taken to cross the river by the shortest path and the quickest path be 4 minutes,the width of the river is (in km)
View Solution
Knowledge Check
- Question 1 - Select One
A man moves on a cycle with a velocity of 4 km/hr. The rain appears to fall on him with a velocity of 3 km/hr vertically. The actual velocity of the rain is
A7 km/hrB5 km/hrC4/3 km/hrD3/4 km/hr - Question 2 - Select One
A river 2 km wide is flowing at the rate of 2km/hr. A boatman, can row the boat at a speed of 4 km/hr in still water, goes a distance of 2 km upstream and them comes back. The time taken by him to complete his journey is
A60 minutesB70 minutesC80 minutesD90 minutes - Question 3 - Select One
A bird is flying towards south with a velocity 40km/hr and a train is moving with a velocity 40km/hr towards east. What is the velocity of the bird w.r.t. an obserber in train:-
A40√2 km/hr. North-EastB40√2 km/hr. South-EastC40√2 km/hr. South -WestD40√2 km/hr. North-West
A river is flowing with speed 3 km/hr west to east. A man swims with speed 5 km/hr in still water. Man is at south bank of the river. Match the column-1 with direction of velocities of man w.r.t. ground in column-2
 View Solution
View SolutionA man can swim at the rate of 5kmh−1 in still water. A 1−km wide river flows at the rate of 3kmh−1 The man wishes to swim across the river directly opposite to the starting point.
(a) Along what direction must the man swim ?
(b) What should be his resultant velocity ?
( c) How much time will he take to cross the river ?View Solution2 km wide river flowing with a rate of 5 km/hr. A man can swim in the still water with10 km/hr. He wants to cross the river along shortest path find
Crossing timeView SolutionA boat is rowed across a river at the rate of 4.5kmhr. The river flows at the rate of 6kmhr. The velocity of boat in ms is:
View SolutionA river is flowing with a speed of 1 km/hr. A swimmer wants to go to point C starting from A. He swims with a speed of 5km/hr. at an angle θ. W.r.t. the river flow. If AB=BC=400m at what angle with river tank shou ld swimmer swim?
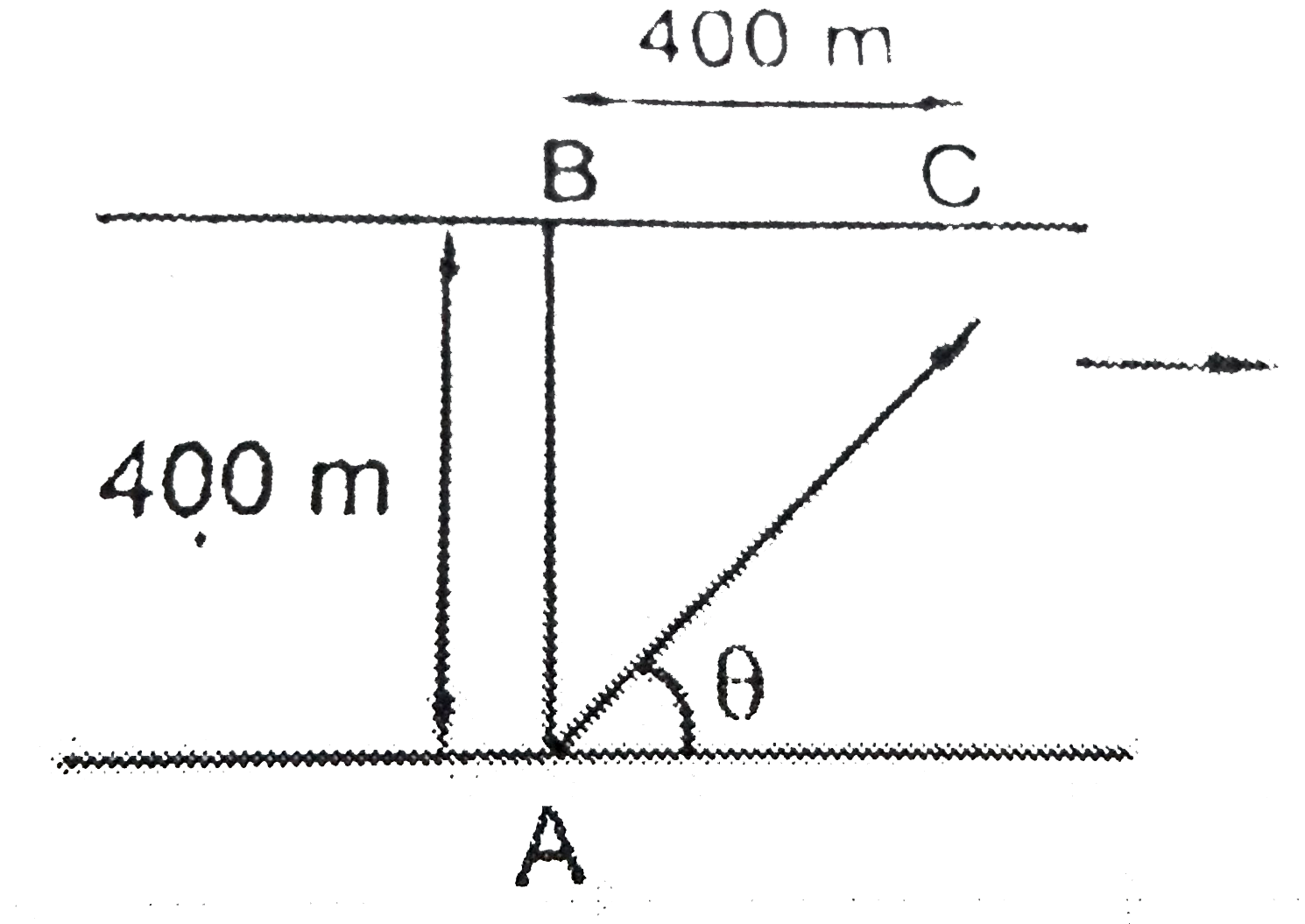 View Solution
View Solution

