The terminal voltage is E2 when a c urrent of 2A is flowing through 2Ω resistance, then the internal resistance of cell is:-
1Ω
2Ω
3Ω
4Ω
The correct Answer is:2
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the Problem
We have a circuit with a battery (with EMF E), a current of 2A flowing through a 2Ω resistor, and the terminal voltage of the battery is given as E2. We need to find the internal resistance r of the battery.
Step 2: Write Down the Known Values
- Current (I) = 2A
- Resistance (R) = 2Ω
- Terminal Voltage (V) = E2
Step 3: Apply the Formula for Terminal Voltage
The terminal voltage V can be expressed using the formula:
V=E−I⋅r
Where:
- E = EMF of the battery
- r = internal resistance of the battery
Step 4: Substitute Known Values into the Formula
Since we know that V=E2, we can substitute this into the equation:
E2=E−I⋅r
Substituting I=2A:
E2=E−2r
Step 5: Rearrange the Equation
Now, let's rearrange the equation to isolate r:
2r=E−E2
This simplifies to:
2r=E2
Step 6: Solve for Internal Resistance r
Now, divide both sides by 2:
r=E4
Step 7: Find the Value of E
To find E, we can use the voltage drop across the 2Ω resistor:
V=I⋅R=2A⋅2Ω=4V
Since V=E2:
E2=4V
Thus:
E=8V
Step 8: Substitute E Back to Find r
Now substitute E=8V back into the equation for r:
r=8V4=2Ω
Conclusion
The internal resistance of the cell is r=2Ω.
---
We have a circuit with a battery (with EMF E), a current of 2A flowing through a 2Ω resistor, and the terminal voltage of the battery is given as E2. We need to find the internal resistance r of the battery.
- Current (I) = 2A
- Resistance (R) = 2Ω
- Terminal Voltage (V) = E2
The terminal voltage V can be expressed using the formula:
V=E−I⋅r
Where:
- E = EMF of the battery
- r = internal resistance of the battery
Since we know that V=E2, we can substitute this into the equation:
E2=E−I⋅r
Substituting I=2A:
E2=E−2r
Now, let's rearrange the equation to isolate r:
2r=E−E2
This simplifies to:
2r=E2
Now, divide both sides by 2:
r=E4
To find E, we can use the voltage drop across the 2Ω resistor:
V=I⋅R=2A⋅2Ω=4V
Since V=E2:
E2=4V
Thus:
E=8V
Now substitute E=8V back into the equation for r:
r=8V4=2Ω
The internal resistance of the cell is r=2Ω.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A cell of 2.1 V gives 0.2 A current through resistance 10Ω The internal resistance is:
A5ΩB50ΩC0.05ΩD0.5Ω - Question 2 - Select One
In the shown figure, bridge is balanced, the current flowing through 2Ω resistance is
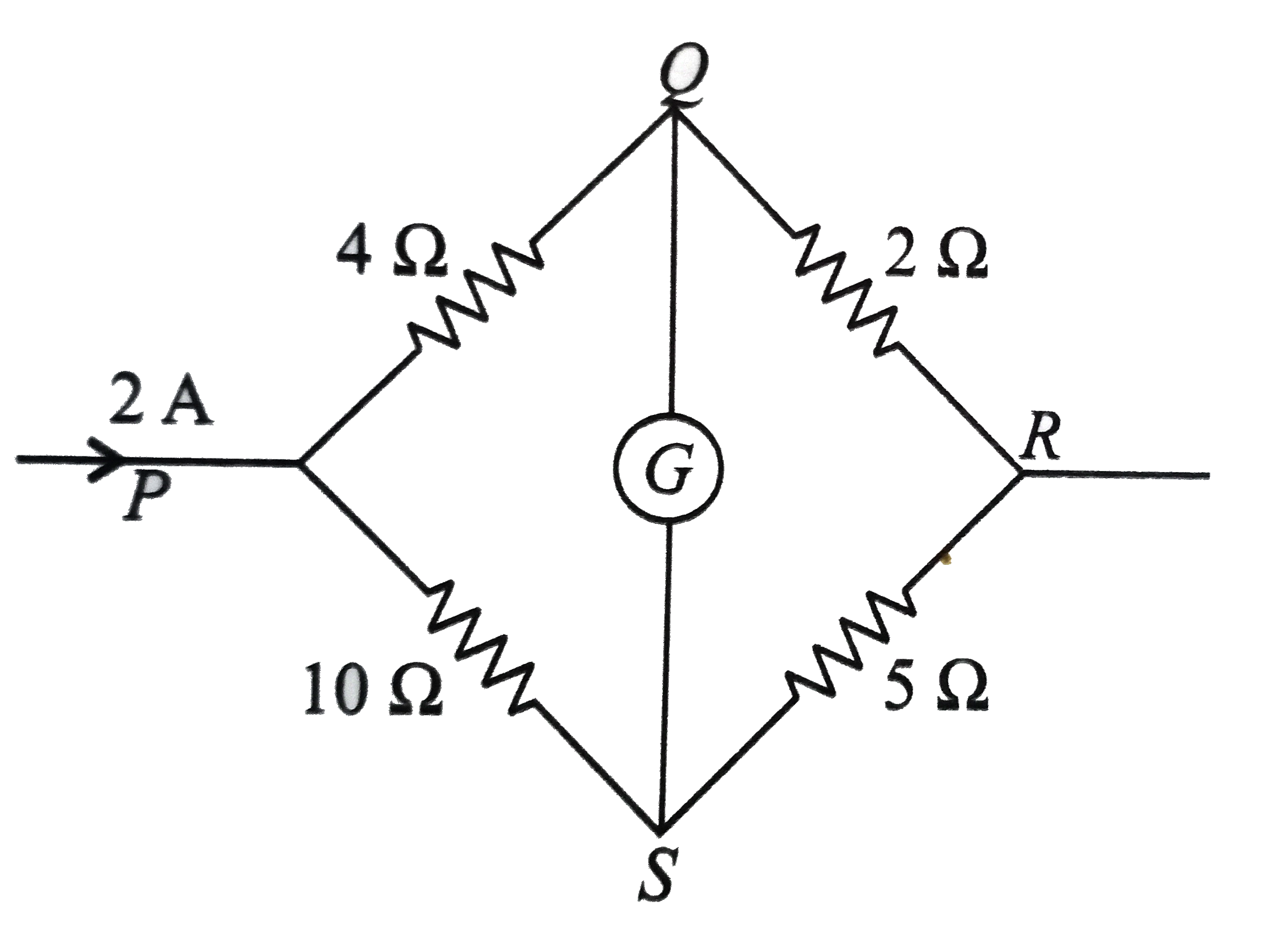 A107AB117AC137AD87A
A107AB117AC137AD87A - Question 3 - Select One
Two similar cells, whether joined in series or in parallel, have the same current through an external resistance of 2Ω . The internal resistance of each cell is :
A1ΩB2ΩC0.5ΩD1.5Ω
The potential difference across terminals of a battry is 9.0V, when a current of 3.5A flows through it from its negative terminal to the positive terminal .When a current of 2A flows through in the opposite direction, the terminal potential difference is 12V. Find the internal resistance and emf of the battery
View SolutionIn an experiment to measure the internal resistance of a cell by a potentiometer, it is found that the balance point is at a length of 2m when the cell is shunted by a 5Ω resistance and is at a length of 3m when the cell is shunted by a 10Ω resistance, the internal resistance of the cell is then
View SolutionFor a cell terminal potential difference is 2.2 V when circuit is open and reduces to 1.8V when cell is connected to a resistance of R=5Ω then determine internal resistance of cell is:-
View SolutionIn an experiment to measure the internal resistance of a cell by potentiometer, it is found that the balance point is at a length of 2 m when the cell is shunted by a 4Ω resistance and at 3 m when cell is shunted by a 8Ω resistance. The internal resistance of cell is -
View SolutionFor a cell, the terminal potential difference is 2.2V, when circuit is open and reduces to 1.8V. When cell is connected to a resistance R=5Ω, the internal resistance of cell (R) is
View Solution