A ring is made of a wire having a resistance R0=12Ω. Find the point A and B, as shown in the figure, at which a current carrying conductor should be connected so that the resistance R of the subcircuit between these points is equal to 83Ω
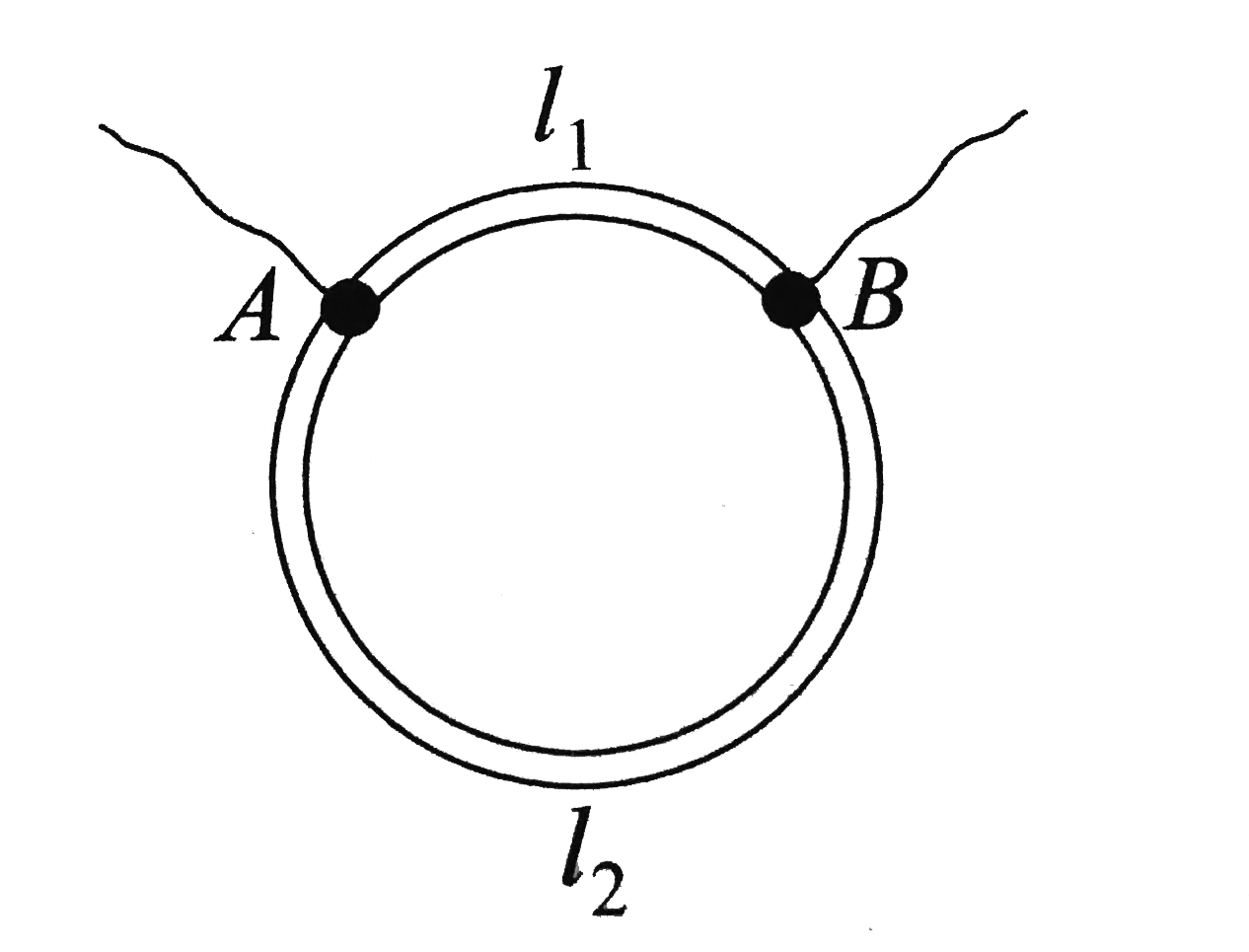
l1l2=38
l1l2=12
l1l2=58
l1l2=13
The correct Answer is:2
R1R2R1+R2=83&R1+R2=12⇒R1R2=32
⇒R2−R1=√(R1+R2)2−4R1R2
=√122−4×32=4Ω
So R1=4Ω and R2=8Ω
Hence l1l2=48=12
Topper's Solved these Questions
Similar Questions
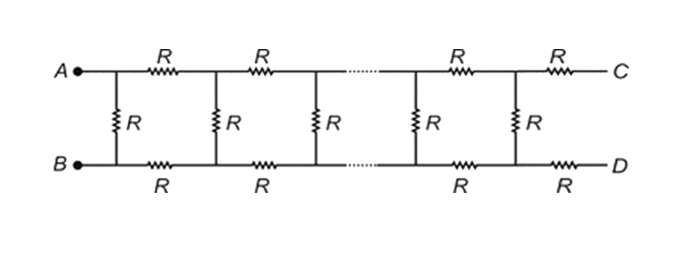
In the circuit shown, the resistance of each of resistor is R=100Ω. Find the nearest integer, which is to be connected points C and D so that the resistance of entire ciruit between A and B does not depend on the number of elementary cells.
 View Solution
View SolutionFive equal resistors each of RΩ are connected in a network. Calculate the equivalent resistance between the points A and B.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Five equal resistances of 10Ω are connected between A and B as shown in figure. The resultant resistance
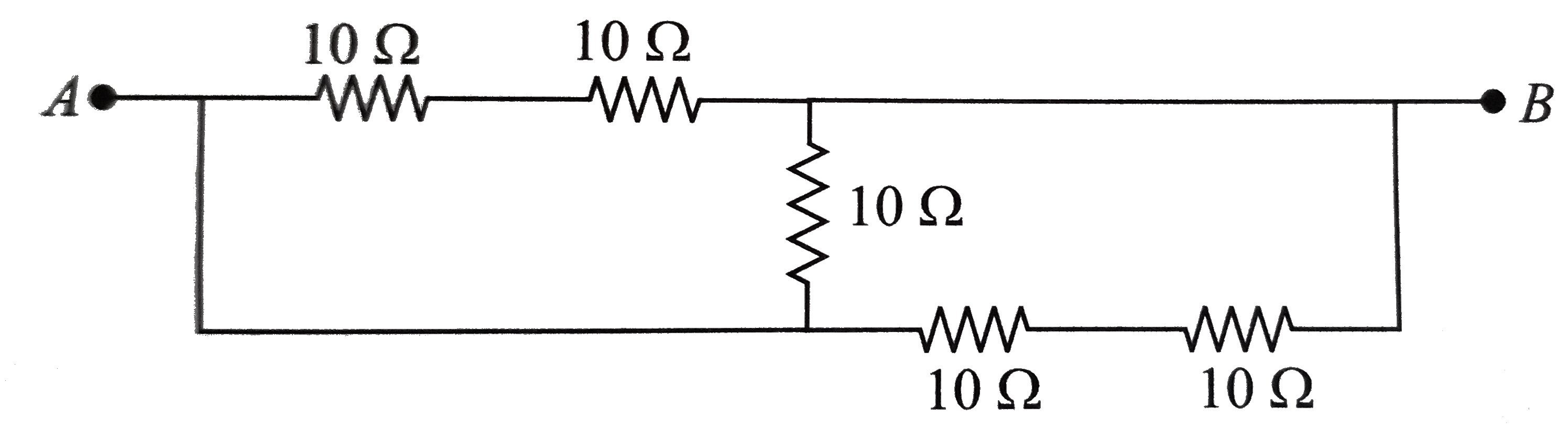 A10ΩB5ΩC15ΩD6Ω
A10ΩB5ΩC15ΩD6Ω - Question 2 - Select One
A wire has linear resistance ρ (inΩm−1). Find the resistance R between points A and B if the side of the big square is d.
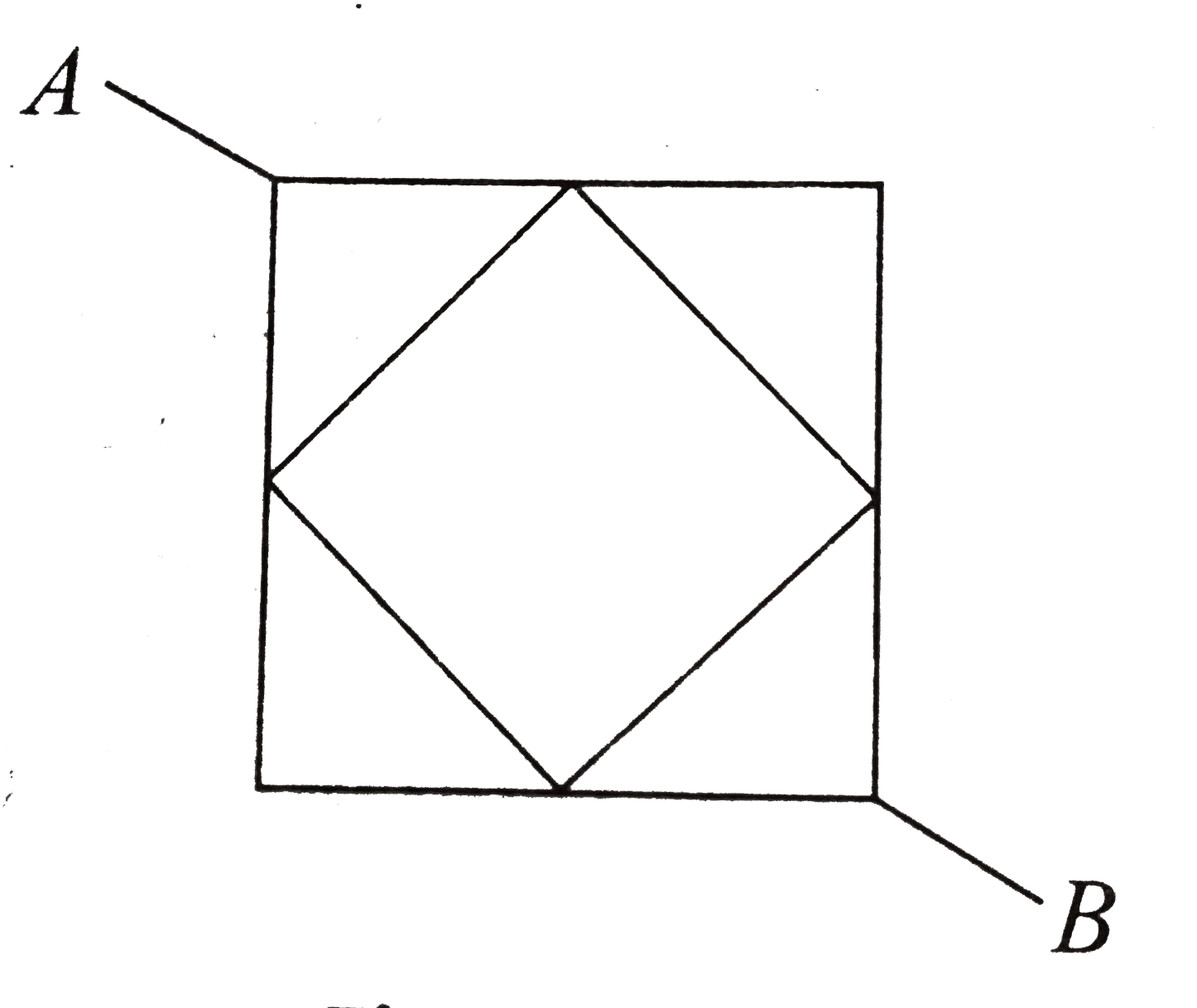 Aρd√2B(√2)ρdC2ρdDnone of these
Aρd√2B(√2)ρdC2ρdDnone of these - Question 3 - Select One
In the network shown in the figure, each of the resistance is equal to 2Ω. The resistance between the points A and B is
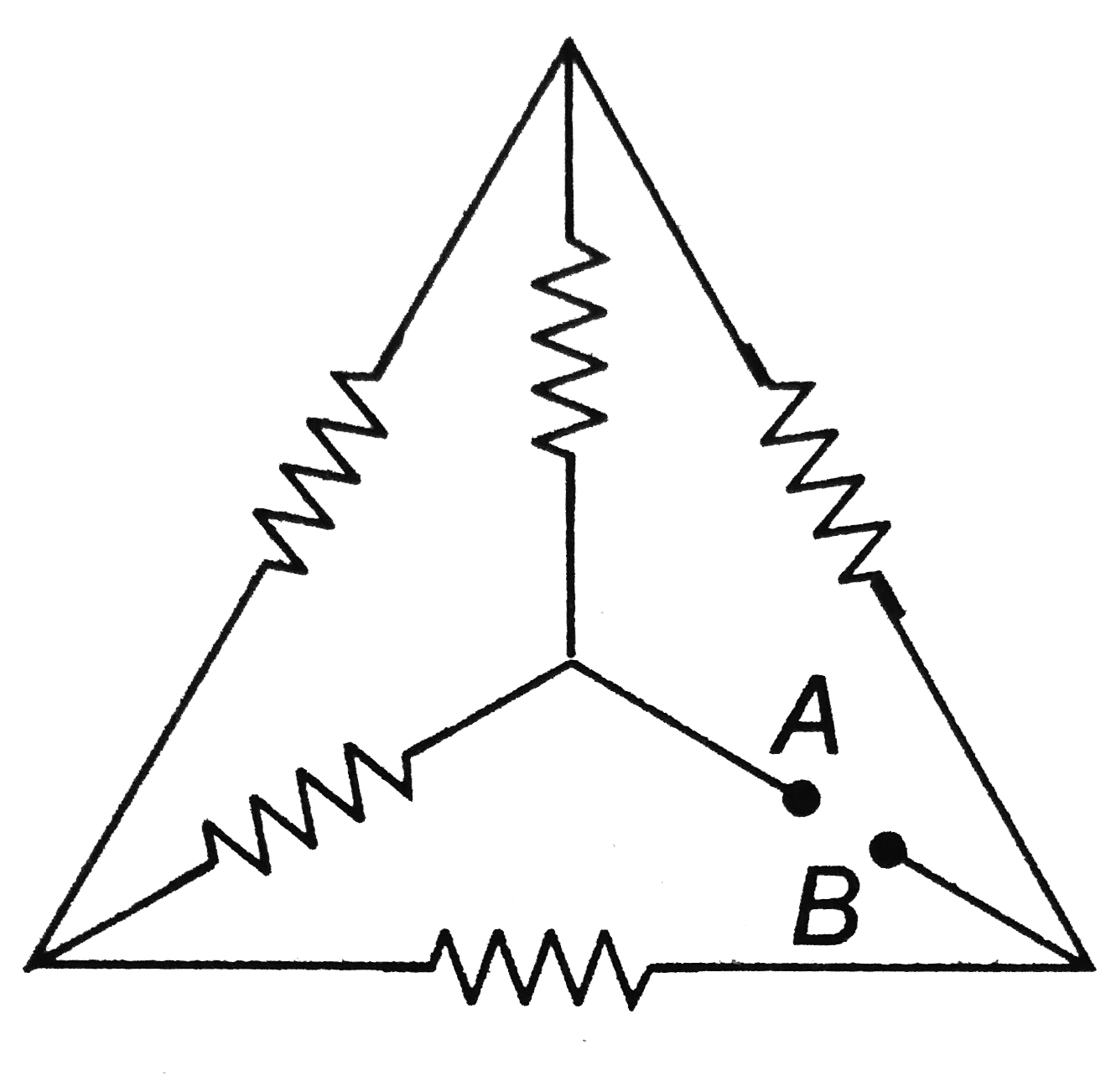 A1ΩB4ΩC3ΩD2Ω
A1ΩB4ΩC3ΩD2Ω
In the network shown in the figure, each of the resistance is equal to 2Ω . The resistance between the point A and B is
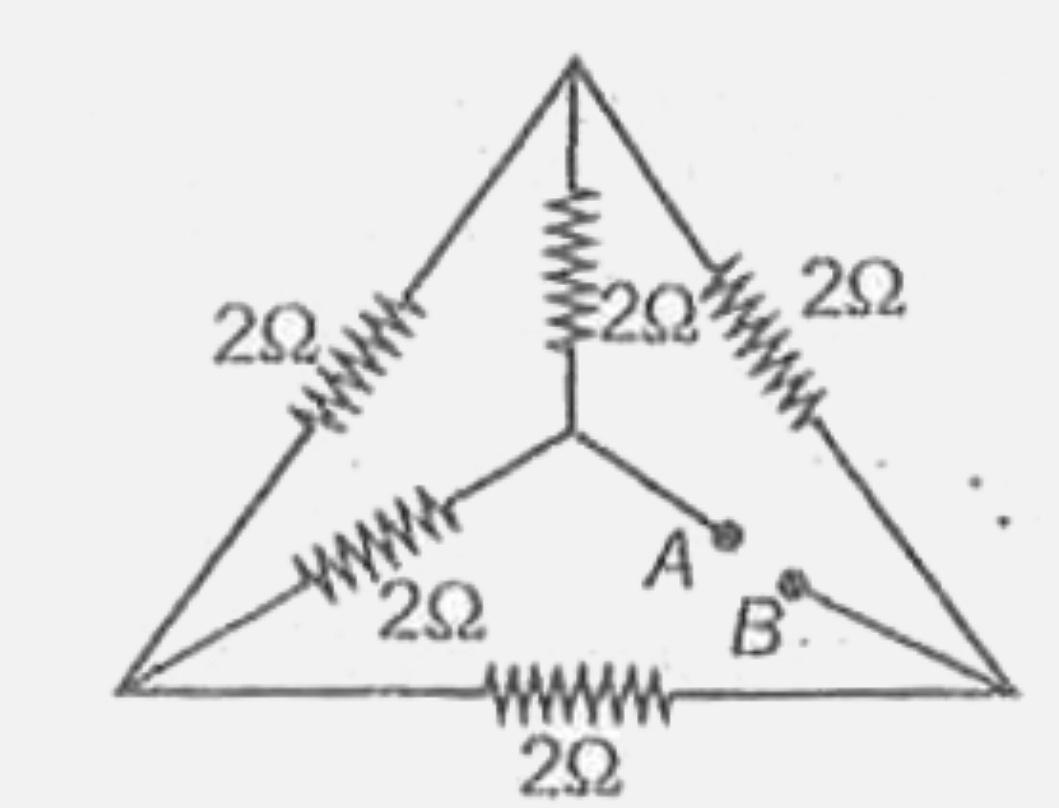 View Solution
View Solution
Six equal resistances are connected between points P, Q and R as shown in the figure. Then the net resistance will be maximum betweenView SolutionThe effective resistance (in Ω) between P and R of letter A containing resistances as shown in the figure is:
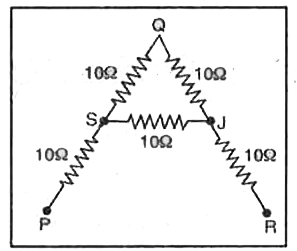 View Solution
View SolutionA battery of internal resistance 4Ω is connected to the network of resistance as shown . In order that the maximum power can be delivered to the network, the value of R in Ω should be
 . View Solution
. View SolutionThe network shown in figure is an arrangement of nine identical resistors. The resistance of the network between points A and B is 1.5Ω. The resistance r is
 View Solution
View Solution

