Two resistance connected in parallel across a cell of negligible internal resistance, use 4.5 times the power that they would use, when in series across the same cell. If one of the resistance is 8ohm, the other is:-
8Ω
12Ω
16Ω
36Ω
To solve the problem, we need to find the value of the second resistance R2 given that one resistance R1=8Ω and the power used in parallel is 4.5 times the power used in series.
1. Understanding Power in Series and Parallel:
- The power Ps in series is given by:
Ps=V2R1+R2
- The power Pp in parallel is given by:
Pp=V2R1R2R1+R2
- This can be rewritten as:
Pp=V2(R1+R2)R1R2
2. Setting Up the Equation:
- According to the problem, Pp=4.5×Ps:
V2(R1+R2)R1R2=4.5×V2R1+R2
- We can cancel V2 from both sides (since V is not zero):
R1+R2R1R2=4.5×1R1+R2
3. Cross-Multiplying:
- Cross-multiplying gives:
(R1+R2)2=4.5×R1R2
4. Substituting Known Values:
- Substitute R1=8Ω:
(8+R2)2=4.5×8×R2
- This simplifies to:
(8+R2)2=36R2
5. Expanding and Rearranging:
- Expanding the left side:
64+16R2+R22=36R2
- Rearranging gives:
R22−20R2+64=0
6. Using the Quadratic Formula:
- We can solve this quadratic equation using the quadratic formula R2=−b±√b2−4ac2a:
- Here, a=1,b=−20,c=64:
R2=20±√(−20)2−4⋅1⋅642⋅1
R2=20±√400−2562
R2=20±√1442
R2=20±122
7. Calculating the Values:
- This gives two possible solutions:
R2=322=16ΩorR2=82=4Ω
8. Conclusion:
- Since both resistances are connected in parallel, the second resistance R2 must be 16 ohms to satisfy the condition given in the problem.
Final Answer:
The other resistance is R2=16Ω.
- The power Ps in series is given by:
Ps=V2R1+R2
- The power Pp in parallel is given by:
Pp=V2R1R2R1+R2
- This can be rewritten as:
Pp=V2(R1+R2)R1R2
- According to the problem, Pp=4.5×Ps:
V2(R1+R2)R1R2=4.5×V2R1+R2
- We can cancel V2 from both sides (since V is not zero):
R1+R2R1R2=4.5×1R1+R2
- Cross-multiplying gives:
(R1+R2)2=4.5×R1R2
- Substitute R1=8Ω:
(8+R2)2=4.5×8×R2
- This simplifies to:
(8+R2)2=36R2
- Expanding the left side:
64+16R2+R22=36R2
- Rearranging gives:
R22−20R2+64=0
- We can solve this quadratic equation using the quadratic formula R2=−b±√b2−4ac2a:
- Here, a=1,b=−20,c=64:
R2=20±√(−20)2−4⋅1⋅642⋅1
R2=20±√400−2562
R2=20±√1442
R2=20±122
- This gives two possible solutions:
R2=322=16ΩorR2=82=4Ω
- Since both resistances are connected in parallel, the second resistance R2 must be 16 ohms to satisfy the condition given in the problem.
The other resistance is R2=16Ω.
Topper's Solved these Questions
Similar Questions
A voltmeter of resistance R1 and an ammeter of resistance R2 are connected in series across a battery oif negligible internal resistance. When as resistance R is connected in parallel to voltmeter reading of ammeter increases three times white that of voltmeter reduces to one third. Find R1 and R2 in terms of R.
View SolutionA voltmeter of resistance 995Ω is connected across a cell of emf 3V and internal resistance 5Ω. Find the potential difference across the voltmeter, that across the terminals of the cell and percentage error in the reading of voltmeter.
View Solution
Knowledge Check
Two resistances , connected in parallel across a source of negligible interna resistance, consumes four times the power that they would consume when connected in series across the same source. If one of the resistances is 10Ω the other is
A5ΩB10ΩC20ΩD40ΩAn ammeter and a voltmeter of resistance R connected in seires to an electric cell of negligible internal resistance. Their readings are A and V respecitvely. If another resistance R is connected in parallel with the voltmeter
ABoth A and V will increaseBBoth A and V will decreaseCA will decrease and V will increaseDA will decrease and V will decreaseAn ammeter and a voltmeter of resistance R are connected in series to an electric cell of negligible internal resistance . Their readings are A and V respectively. If another resistance R is connected in parallel with the voltmeter , then
ABoth A and V increasesBBoth A and V decreasesCA decreases but V increasesDA increases but V decreases.
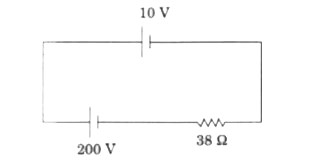
A 10 V cells of negligible internal resistance is connected in parallel across a battery of emf 200 V and internal resistance 38Q . As shown in the figures , Find the value of current in the circuit
In a potentiometer arrangement for determining the emf . of a cell the balance point of the cell in open circuit is 350 cm. When a resistance of 9Q . is used in the external circuit of the cells the balance point shift to 300 cm. Determine the internal resistance of the cell.
View SolutionWhen two resistors are connected in series with a cell of emf 2 V and negligible internal resistance, a current of 25A flows in the circuit. When the resistors are connected in parallel the main current is 53A. Calculate the resistances.
View SolutionAn ammeter and a voltmeter of resistance R are connected in series to an electric cell of negligible internal resistance . Their readings are A and V respectively. If another resistance R is connected in parallel with the voltmeter , then
View SolutionFour equal resistance dissipated 5 W of power together when connected in series to a battery of negligible internal resistance . The total power dissipated in these resistance when connected in parallel across the same battery would be .
View SolutionResistors of 1, 2, 3 ohm are connected in the form of a triangle. If a 1.5 volt cell of negligible internal resistance is connected across 3 ohm resistor, the current flowing through this resistance will be
View Solution
