On dipping one end of a capiilary in liquid and inclining the capillary at an angles 30∘ and 60∘ with the vertical, the lengths of liquid columns in it are found to be l1 and l2 respectively. The ratio of l1 and l2 is
1:√3
1:√2
√2:1
√3:1
The correct Answer is:A
To solve the problem, we need to find the ratio of the lengths of the liquid columns l1 and l2 in a capillary tube inclined at angles 30∘ and 60∘ with the vertical.
1. Understanding the Relationship:
The length of the liquid column in a capillary tube can be expressed as:
l=Hcos(α)
where H is the height of the liquid column when the tube is vertical, and α is the angle of inclination with the vertical.
2. Applying the Formula for Each Angle:
- For l1 (when the angle is 30∘):
l1=Hcos(30∘)
- For l2 (when the angle is 60∘):
l2=Hcos(60∘)
3. Finding the Cosine Values:
- We know that:
cos(30∘)=√32
cos(60∘)=12
4. Substituting the Cosine Values:
- Substitute the cosine values into the expressions for l1 and l2:
l1=H√32=2H√3
l2=H12=2H
5. Finding the Ratio l1l2:
- Now, we can find the ratio:
l1l2=2H√32H
- The 2H terms cancel out:
l1l2=1√3
6. Final Ratio:
- Thus, the ratio l1:l2 is:
l1:l2=1:√3
Conclusion:
The ratio of the lengths of the liquid columns l1 and l2 is 1:√3.
The length of the liquid column in a capillary tube can be expressed as:
l=Hcos(α)
where H is the height of the liquid column when the tube is vertical, and α is the angle of inclination with the vertical.
- For l1 (when the angle is 30∘):
l1=Hcos(30∘)
- For l2 (when the angle is 60∘):
l2=Hcos(60∘)
- We know that:
cos(30∘)=√32
cos(60∘)=12
- Substitute the cosine values into the expressions for l1 and l2:
l1=H√32=2H√3
l2=H12=2H
- Now, we can find the ratio:
l1l2=2H√32H
- The 2H terms cancel out:
l1l2=1√3
- Thus, the ratio l1:l2 is:
l1:l2=1:√3
The ratio of the lengths of the liquid columns l1 and l2 is 1:√3.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If a capillary tube is 45∘and60∘ from the vertical then the ratoio of lengths l1andl2 liquid columns in it will be
A1:√2B√2:1C2:1D1:4 - Question 2 - Select One
A capillary tube when immersed vertically in a liquid records a rise of 6 cm . If the tube is immersed inclined 30∘ with the vertical , then length of liquid column along the tube will be
A2√3cmB4√3cmC4√3cmD12 cm - Question 3 - Select One
In Fig., there are two convex lenses L1 and L2 having focal lengths F1 and F2 respectively. The distance between L1 and L2 will be :
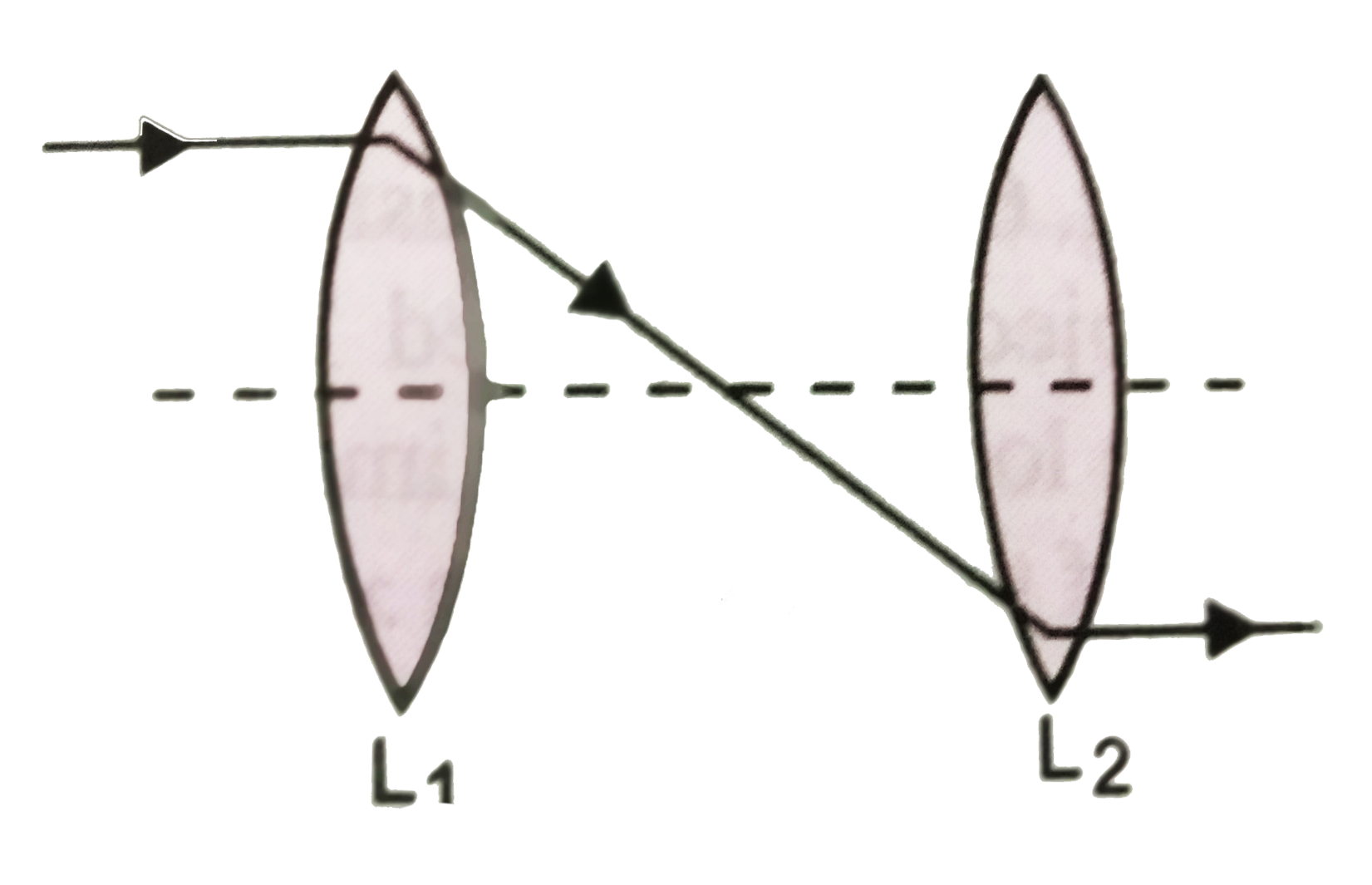 AF1BF2CF1+F2DF1−F2
AF1BF2CF1+F2DF1−F2
In the figure shown, there are two convex lenses L1 and L2 having focal. Lengths f1 and f2 respectively. The distance between L1 and L2 will be
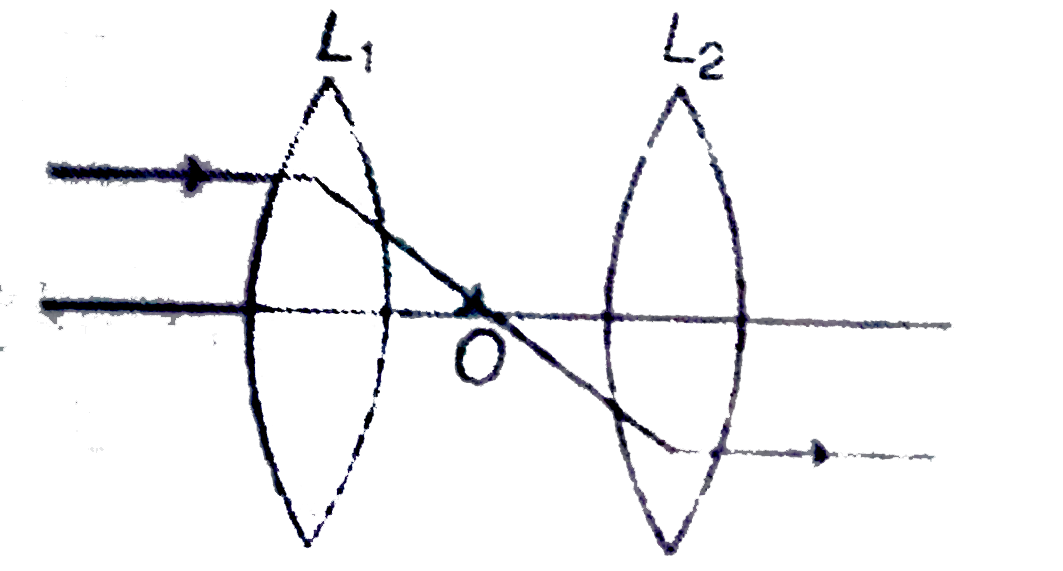 View Solution
View SolutionThe balancing lengths for the cells of e.m.f. E1 and E2 are l1 and l2 respectively. If they are connected separately then
View SolutionIn a pipe opened at both ends n1 and n2 be the frequencies corresponding to vibrating lengths L1 and L2 respectively .The end correction is
View SolutionIn a pipe opened at both ends n1 and n2 be the frequencies corresponding to vibrating lengths L1 and L2 respectively .The end correction is
View SolutionTwo wires of equal diameters, of resistivities ρ1 and ρ2 and length l1 and l2, respectively of the combination is
View Solution


