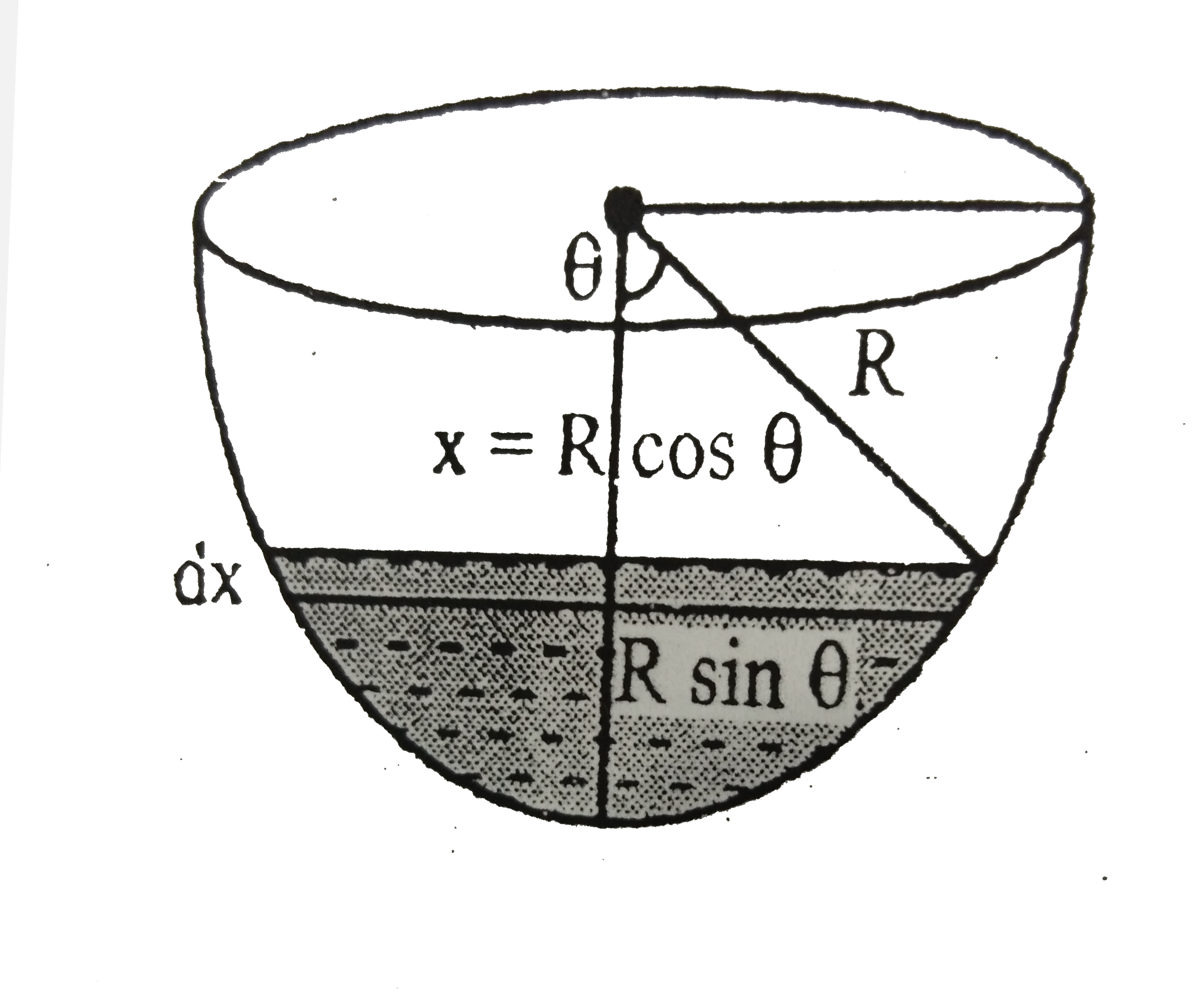
Computer the work which must be performed to slowly pump the water out of a hemispherical reservoir of radius R=0.6m.
The correct Answer is:101.8Kgf−m
W=∫(dm)gx
W=∫π(Rsinθ)2dxρg(Rcosθ) ……(1)
since x=Rcosθ
so, dx=−Rsinθdθ …..(2)
From (1) and (2)
W=0∫π/2π(Rsinθ)2(−Rsinθdθ)ρg(Rcosθ)
W=−πRρ4g0∫π/2sin3θcosθdθ
put sinθ=t so,cosθdθ=dt
W=−πRρ4g0∫π/2t3dt W=−πR4ρg4[t4]0π/2
W=πR4g4[sin4θ]0π/2 =W=πR4ρg4
W=3.14×(0.6)4×1000×g4⇒W=101.8kgf−m
Topper's Solved these Questions
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:EXERCISE # II
Explore 18 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:EXERCISE # III
Explore 18 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:PYQS AIEEE
Explore 10 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Additional topic
Explore 70 Videos
Similar Questions
Knowledge Check
A small block of mass m os takes slowly up a fixed hemisphere from P to Q and then slowly down along its surface from Q to S by force F, which at each point of the surface, is tangential to the surface. If the coefficient of friction is μ, then the work performed by the force F in taking the block from P to S along the hemispherical surface of radius R is :
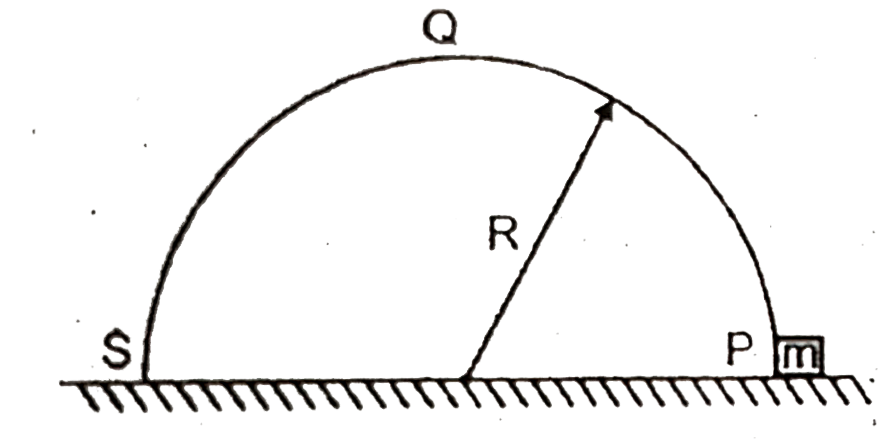 A2μmgRBμmgRCπμmgRDNone of these
A2μmgRBμmgRCπμmgRDNone of theseThe amount of work done in pumping water out of a cubical vessel of height 1 m is nearly
A5000 JB10000 JC50 JD10 J
A small solid sphere of mass m and radius r starting from rest from the rim of a fixed hemispherical bowl of radius R(>>r) rolls inside it without sliding. The normal reaction exerted by the sphere on the hemisphere when it reaches the bottom of hemisphere isA(3/7)mgB(9/7)mgC(13/7)mgD(17/7)mg
Find the work to be performed in order to blow a soap bubble of radius R if the outside air pressure is equal to p0 and the surface tension of the soap water solution is equal to α.
View SolutionCalculate the gravitational potential at the centre of base of a solid hemisphere of mass M, radius R.
View SolutionCalculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass m, radius R
View SolutionWater is flowing out at the rate of 6m3min from a reservoir shaped like a hemispherical bowl of radius R=13m. The volume of water in the hemispherical bowl is given by V=π3.y2(3R−y)when the water is y meter deep. Find
View SolutionThe amount of work done in pumping water out of a cubical vessel of height 1 m is nearly (g=10ms−2)
View Solution
