A solid sphere of radius $R$ is floating in a liquid of density $σ$ with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $f = \frac{1}{2 π} \sqrt{\frac{3 g}{2 R}}$

Weight = Buoyancy
$\frac{4}{3} π R^{3} σ g = \frac{2}{3} π R^{3} ρ g \Rightarrow σ = \frac{ρ}{2}, σ$ =density of shpere
when sphere is slightly pushed down by x and released. Restoring force will be provioded by extra buoyancy.
$F_{R} = - (π R^{2} x) ρ g \Rightarrow F_{R} = - π R^{2} ρ g x$
$k = π R^{2} ρ g$
$n = \frac{1}{2} π \sqrt{\frac{k}{m}} \Rightarrow n = \frac{1}{2} π \sqrt{\frac{π R^{2} ρ g}{\frac{4}{3} π R^{3} σ}} \Rightarrow n = \frac{1}{2} π \sqrt{\frac{3}{4} \frac{ρ}{σ} \frac{g}{R}}$
by putting the value of $σ$ , we get, $n = \frac{1}{2} π \sqrt{\frac{3 g}{2 R}}$

|

Updated on:21/07/2023

Class 12 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A solid sphere of density $σ$ with one -third of tis volume submerged . When the sphere is pressed down slightly and released , it executes S.H.M of time period T. Then (viscous effect is ignored)
A $p = \frac{σ}{3}$
B $p = 3 σ$
C $\frac{4 π}{3} \sqrt{\frac{R}{g}}$
D $\frac{3 π}{2} \sqrt{\frac{R}{g}}$
Question 2 - Select One
A pendulum of mass $m$ and length $L$ is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is

A $\sqrt{\frac{g}{L}}$
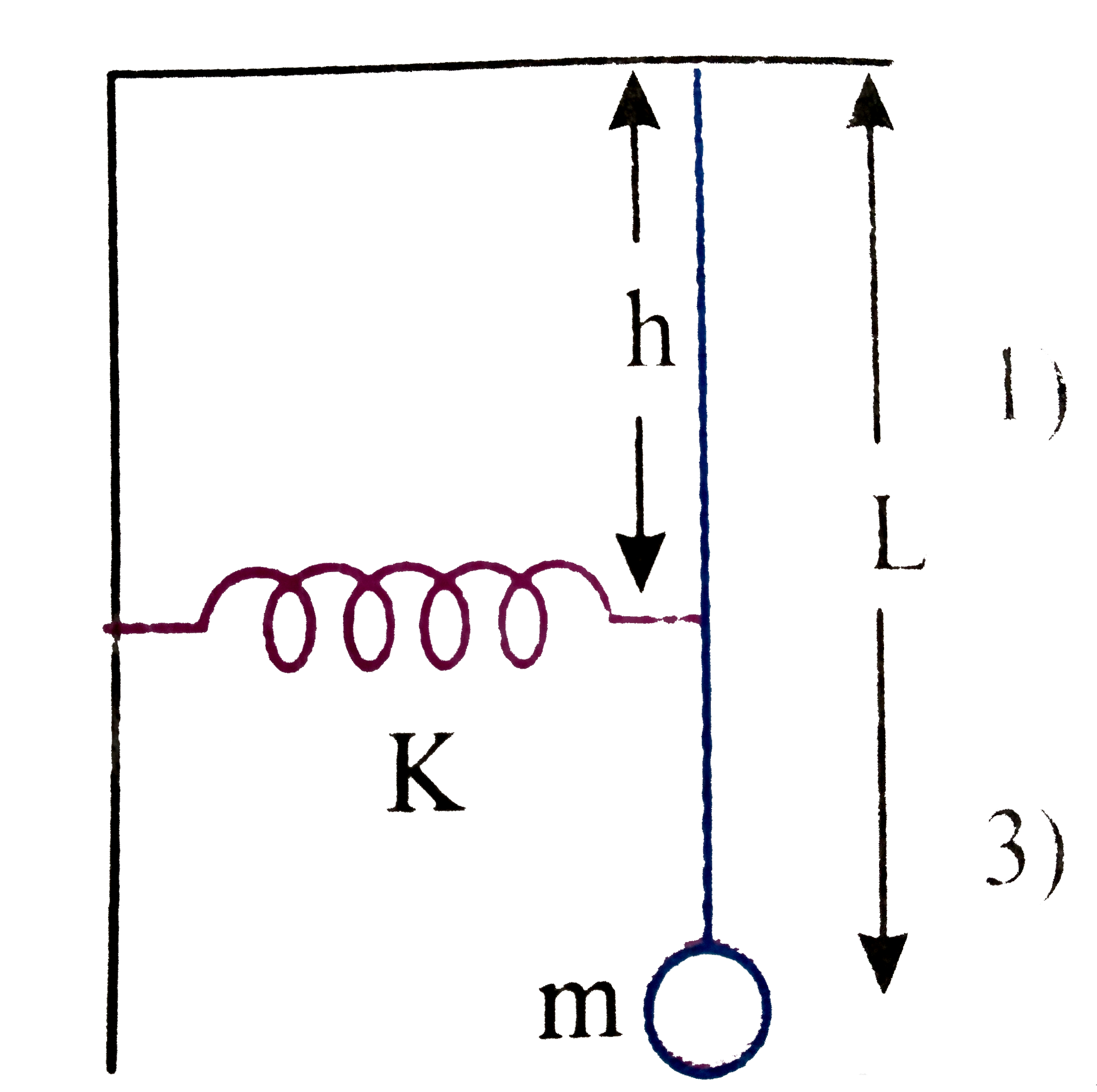B $\sqrt{\frac{K h^{2} + m g L}{m L^{2}}}$
C $\frac{\sqrt{3 g}}{L}$
D $\sqrt{\frac{K h^{2}}{m L^{2}}}$
Question 3 - Select One
A uniform solid bar of wood floats vertically in water with 10 cm of its height immersed in the water. When it is slightly depressed and released, it oscillates with a frequency of
A $\frac{π}{7} H z$
B $\frac{\sqrt{2 π}}{7} H z$
C $\frac{7}{π} H z$
D $\frac{7}{\sqrt{2 π}} H z$

BANSAL-FLUID MECHANICS-EXERCISE # III

Home
Ask Doubt
Profile