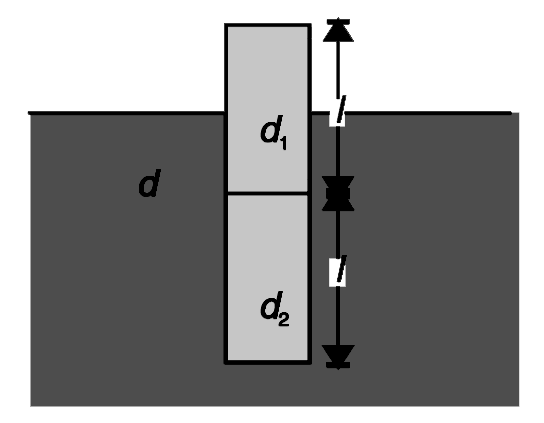
A cylindrical block of length 2l is made of two different materials. T

When a body of density $d_{1}$ and volume V is floating in a liquid of density $d_{2}$
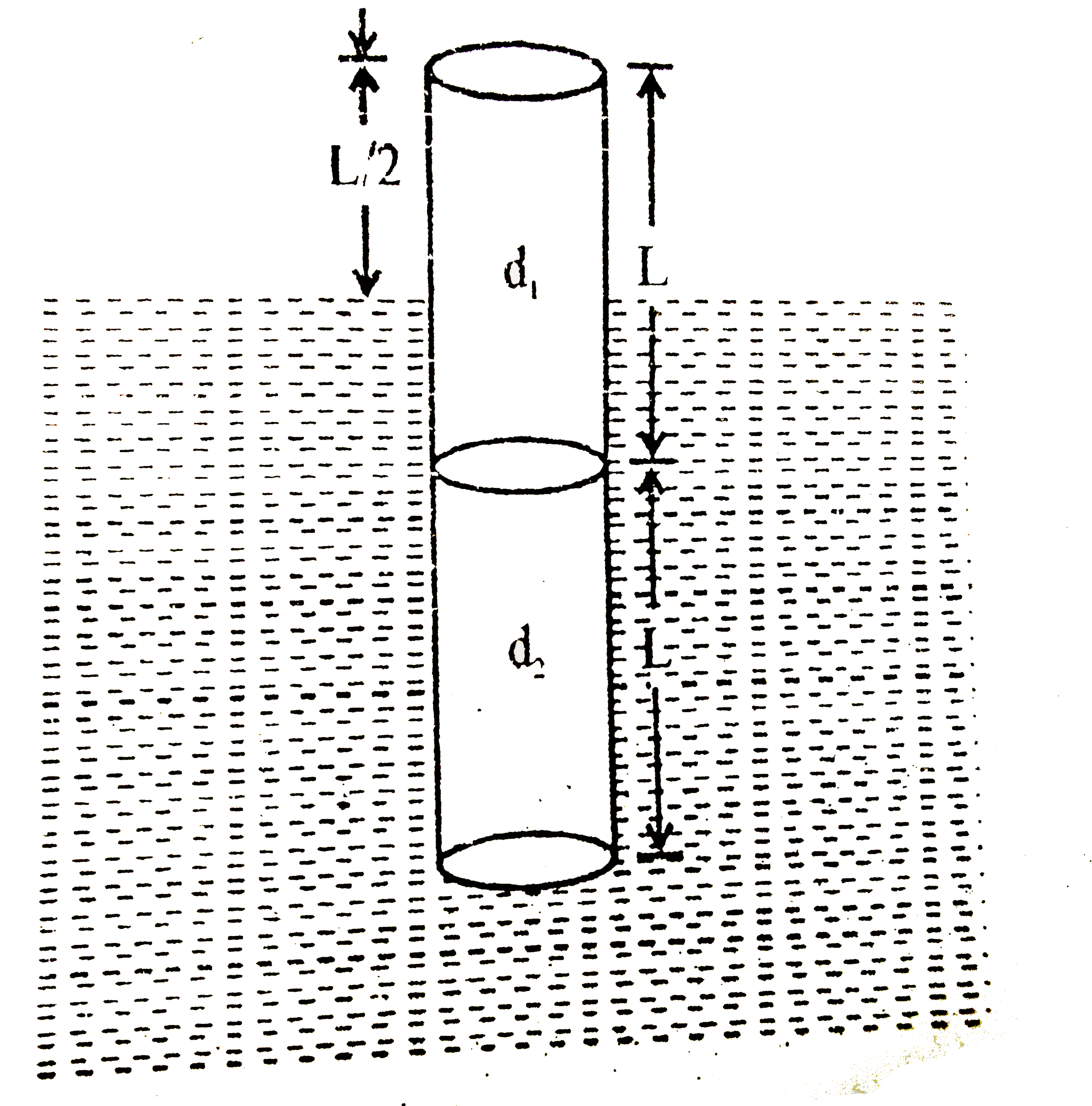
Aits true weight is $V d_{2} g$
Bloss in its weight is $V d_{2} g$
Cits apparent weight is zero
Dits density $d_{1}$ is greater than that of liquid $d_{2}$ .
Two cylinders of same cross-section and length L but made of two different materials of densities $d_{1}$ and $d_{2}$ are cemented together to from a cylinder of length 2L. The combination floats in a liquid of density $d d_{1} < d_{2}$ then
A $d_{1} < \frac{3}{4} d$
B $\frac{d}{2} > d_{1}$
C $\frac{d}{4} > d_{1}$
D $d < d_{1}$
An object weights $m_{1}$ in a liquid of density $d_{1}$ and that in liquid of density $d_{2}$ is $m_{2}$ . The density of the object is
A $\frac{m_{2} d_{2} - m_{1} d_{1}}{m_{2} - m_{1}}$
B $\frac{m_{1} d_{1} - m_{2} d_{2}}{m_{2} - m_{1}}$
C $\frac{m_{2} d_{1} - m_{1} d_{2}}{m_{1} - m_{2}}$
D $\frac{m_{1} d_{2} - m_{2} d_{1}}{m_{1} - m_{2}}$

The correct Answer is:A