Question

A particle of mass $\text{'}m\text{'}$ is moving in the $x-y$ plane such that its $x$ and $y$ coordinate very according to the law $x=a\sin \omega t$ and $y=a\cos \omega t$ where $\text{'}a\text{'}$ and $\text{'}\omega \text{'}$ are positive constants and $\text{'}t\text{'}$ is time. Find
(a) equation of the path. Name the trajectory (path)
(b) whether the particle moves in clockwise or anticlockwise direction
magnitude of the force on the particle at any time $t$.

Answer

(a) `x^(2) + y^(2) = a^(2)`, circle
(b) The particle moves in clock wise sense.
(C) The magnitude of force `= msqrt(a_(x)^(2) + a_(y)^(2)) = momega^(2)del`

Explanation

(a) `x^(2) + y^(2) = a^(2) (sin^(2)omegat + cos^(2)(omegat)) = a^(2)`
Hence the particle moves in a circle of radius `'a'` with centre at origin.
(b) At `t = 0` sec, `x = 0` and `y = +a`. Hence the particle is at `P` as shown in figure.

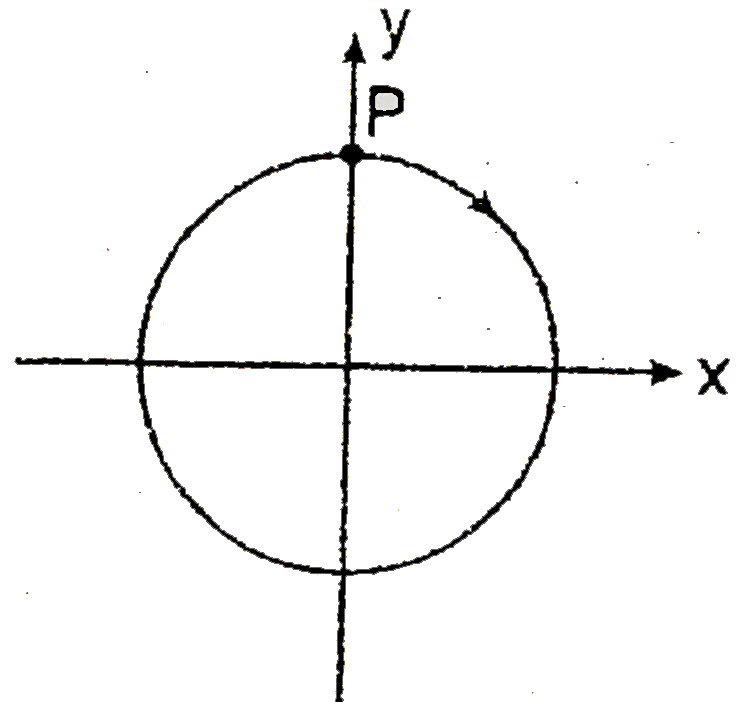
As `'t'` increases `'x'` increases and `'y'` decreases
`:.` the particle moves in clock wise sense.
(c) The `'x'` and `'y'` compoenents of acceleration are
`a_(x) = (d^(2)x)/(dt^(2)) = - omega^(2)x , a_(y) = (d^(2)y)/(dt^(2)) = -omega^(2)y`
The magnitude of force `= m sqrt(a_(x)^(2) + a_(y)^(2)) = momega^(2)a`