Question

After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and $\left|{\psi }^2\right|$ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.

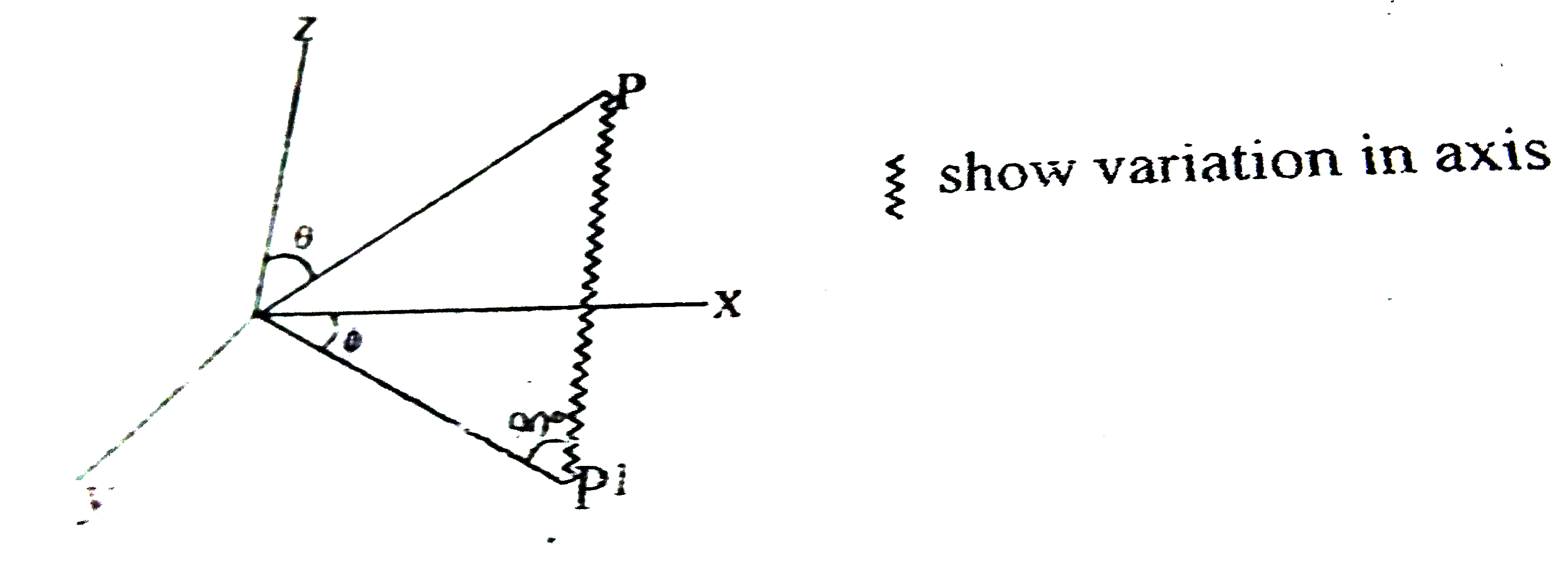
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with $l=0$ are called s-electrons those occupying orbitals for which $l=1$ are p-electrons and those for which $l=2$ are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom $(n=1,l=0)$ we have a $1s$-electron, or that the electron moves in a $1s$-orbital. The relation of the spherical polar co-ordinates $r,\theta$ and $\varphi$ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle $\theta$ and $\varphi$ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
$\varphi (r,\theta ,\varphi )=R\left(r\right)X(\theta ,\varphi )$
Angular and radial parts of hydrogen atom wave function
$(\text{Angular part}X(\theta ,\varphi ),,\text{Radial part}{R}_{n,l}\left(r\right)),(X\left(s\right)={\left(\frac{1}{4\pi }\right)}^{1/2},,R\left(1s\right)=2{\left(\frac{z}{a_0}\right)}^{3/2}{e}^{-\sigma /2}),(X\left(p_x\right)={\left(\frac{3}{4\pi }\right)}^{1/2}\sin \theta \cos \varphi ,,R\left(2s\right)=\frac{1}{2\sqrt{2}}{\left(\frac{z}{a_0}\right)}^{3/2}(2-\sigma )e^{-\sigma /2}),(X\left(p_y\right)={\left(\frac{3}{4\pi }\right)}^{1/2}\sin \theta \sin \varphi ,,R\left(2p\right)=\frac{1}{2\sqrt{6}}{\left(\frac{z}{a_0}\right)}^{3/2}\sigma e^{-\sigma /2}),(X\left(p_z\right)={\left(\frac{3}{4\pi }\right)}^{1/2}\cos \theta ,,),(X\left(d_2^2\right)={\left(\frac{5}{16\pi }\right)}^{1/2}(3{\cos }^2\theta -1),,),(X\left(d_{xz}\right)={\left(\frac{15}{4\pi }\right)}^{1/2}\sin \theta \cos \theta \cos \varphi ,,R\left(3s\right)=\frac{1}{9\sqrt{3}}{\left(\frac{z}{a_0}\right)}^{3/2}(6-6\sigma +{\sigma }^2)e^{-\sigma /2}),(X\left(d_{yz}\right)={\left(\frac{15}{4\pi }\right)}^{1/2}\sin \theta \cos \theta \sin \varphi ,,R\left(3p\right)=\frac{1}{9\sqrt{6}}{\left(\frac{z}{a_0}\right)}^{3/2}(4-\sigma )\sigma e^{-\sigma /2}),(X\left(d_{x^2-y^2}\right)={\left(\frac{15}{4\pi }\right)}^{1/2}{\sin }^2\theta \cos 2\varphi ,,R\left(3d\right)=\frac{1}{9\sqrt{30}}{\left(\frac{z}{a_0}\right)}^{3/2}{\sigma }^2{e}^{-\sigma /2}),(X\left(d_{xy}\right)={\left(\frac{15}{4\pi }\right)}^{1/2}{\sin }^2\theta \sin 2\varphi ,,),(,,\sigma =\frac{2Zr}{n{a}_0},a_0=\frac{h^2}{4{\pi }^{2}m{e}^2})$
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, ${(1/4\pi )}^{1/2}$ regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., ${\psi }^2$ at that point. Thus, ${\psi }^2$ is known as probability density and always a positive quantity.
${\psi }^{2}dV(\text{or}{\psi }^2.4\pi r^{2}dr)$. represents the probability for finding electron in a small volume dV surrounding the nucleus.
The angular wave function of which orbital with not disturb by the variation with azimuthal angle only

Options

A. `1s` and `2s`
B. `2p_(z)` and `2d_(z)^(2)`
C. `2p_(x)` and `3d_(z)^(2)`
D. `2p_(x)` and `2s`

Answer

A