Hydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
Here,
is the Rydberg Constant, is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Determine the loest energy and the radius of the Bohr orbit of the muonic hydrogen atom. Ignore the motion of the nucleus in your calculation. The radius of the Bohr orbit of a hydrogen atom
The classical picture of an ''orbit'' in Bohr's theory has now been replaced by the quantum mechanical nation of an 'orbital'. The orbital for the ground state of a hydrogen atom is given by
where is the distance of the electron from the nucleus and is the Bohr radius.
The correct Answer is:Lowest energy
Radius of the first Bohr orbit
Similar Questions
Hydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion. the wavelength of first line of balmer region.
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Put appropriate channel labels (i) or (ii) in the boxes below
View Solution
Knowledge Check
The observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
1λ=RH[122−1n2]n=3,4,5 . . .
RH=109678cm−1 is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.
The wavelength of first line of Balmer spectrum of hydrogen will be:A4340Ã…B4101Ã…C6569Ã…D4861Ã…The observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
1λ=RH[122−1n2]n=3,4,5 . . .
RH=109678cm−1 is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.
Q.In which region of electromagnetic spectrum does the Balmer series lie?AUVBVisibleCInfraredDFar infrared
Hydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
From the given data, calculate the energy change for the process
H−→H+e−
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
From the given data, calculate the energy change for the process
H−→H+e−
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Determine the values of the dissociation energies (DeineV) of the H2 molecule corresponding to channel (i)
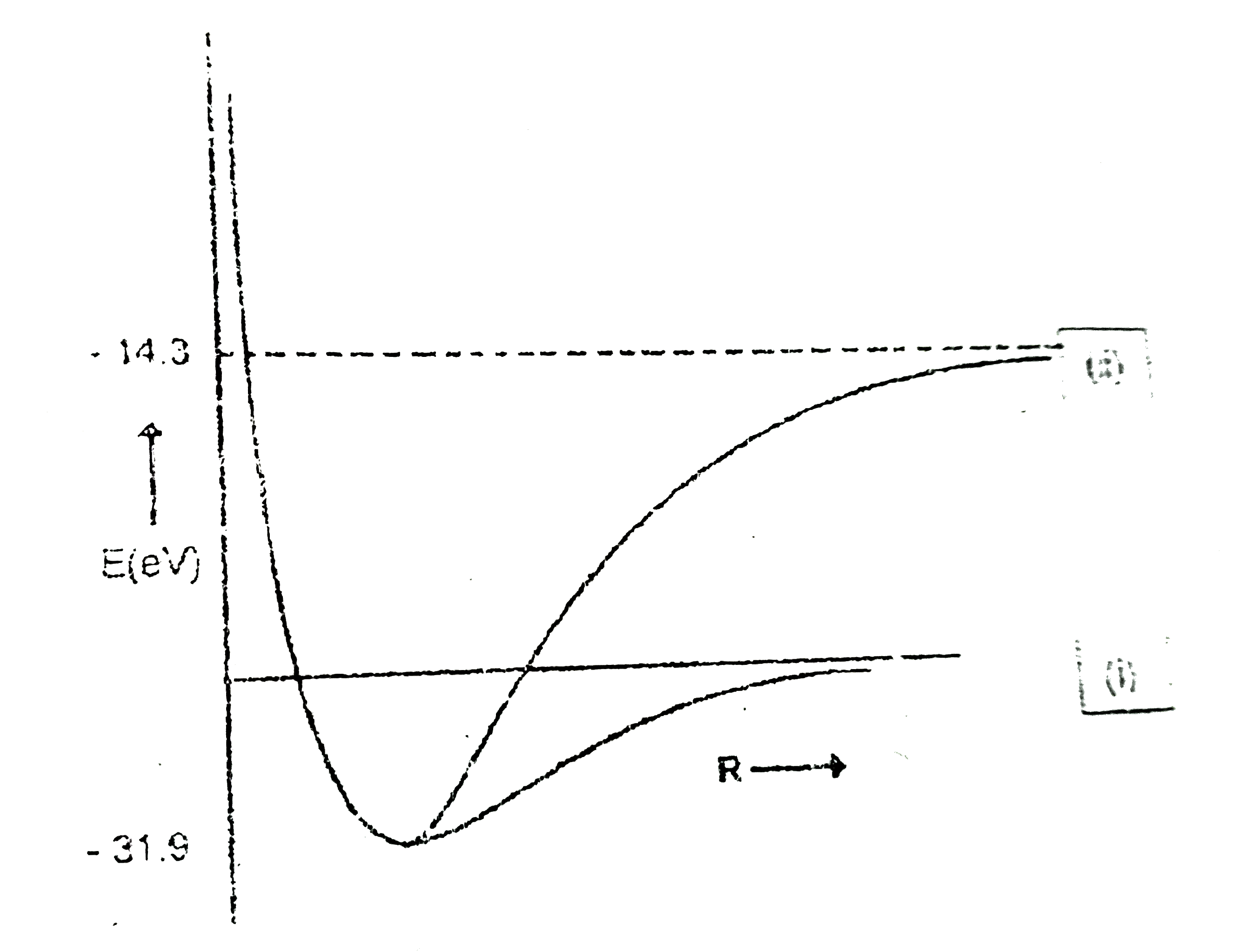
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Calculate the iongest wavelength in A(1Å=10−10m) in the 'Balmer series of singly ionized helium (He+) Ignore nuclear motion in your calculation.
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Calculate the iongest wavelength in A(1Å=10−10m) in the 'Balmer series of singly ionized helium (He+) Ignore nuclear motion in your calculation.
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
H− is a two-electron atomic system. Assuming that the Bohr energy formula is valid for each electron with nuclear charge Z replaced by Zeff' calculate Zeff for H−.
View Solution
