One mole of an ideal mono-atomic gas is caused to go through the cycle shown in the figure below. Then the change in the internal enegry in expanding the gas from a to c along the path abc is:

3P0V0
6RT0
4.5RT0
10.5RT0
The correct Answer is:D
Pv=nRT at point C
2P0×4V0=1×RTc
Tc=[8P0V0R]
at point a
P0V0=1×RT0
T0=P0V0R,Tc=8T0
change in internal energy =[nCvdT]
For path a to b=1×32R×[3T0)=92RT0
For path b to c=1×32R×[4T0]=6T0R
Total change =92RT0+6RT0=21RT02=10.5RT0
So total change in internal energy
ΔU=10.5RT0
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - THERMODYNAMICSEXERCISE - A-11videos
THERMODYNAMICS
- BOOK - RESONANCECHAPTER - THERMODYNAMICSEXERCISE - A-21videos
THERMODYNAMICS
- BOOK - RESONANCECHAPTER - THERMODYNAMICSEXERCISE - exercise-3 part-III Advanced level Solutions (STAGE-II)45videos
THERMODYNAMICS
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - CHEMISTRY50videos
TEST SERIES
Similar Questions
One mole of an ideal monoatomic gas is put throught reverslible path as show in figure .Fill in the blank
in the table given below :
 View Solution
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process as shown in figure. Then the change in the energy in expanding the gas from a to c along the path abc is:
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
One mole of an ideal mono-atomic gas is caused to go through the cycle shown in the figure below. Then the change in the internal enegry in expanding the gas from a to c along the path abc is:
 A3P0V0B6RT0C4.5RT0D10.5RT0
A3P0V0B6RT0C4.5RT0D10.5RT0 - Question 2 - Select One
One mole of an ideal monoatomic gas is caused to go through the cycle shown in figure.Then the change in the internal energy of gas from a to b and b to c is respectively :
 A9P∘V∘2,6RT∘B9P∘V∘2,10RT∘C15P∘V∘2,6RT∘D15P∘V∘2,10RT∘
A9P∘V∘2,6RT∘B9P∘V∘2,10RT∘C15P∘V∘2,6RT∘D15P∘V∘2,10RT∘ - Question 3 - Select One
Ideal gas is taken through the process shown in the figure :
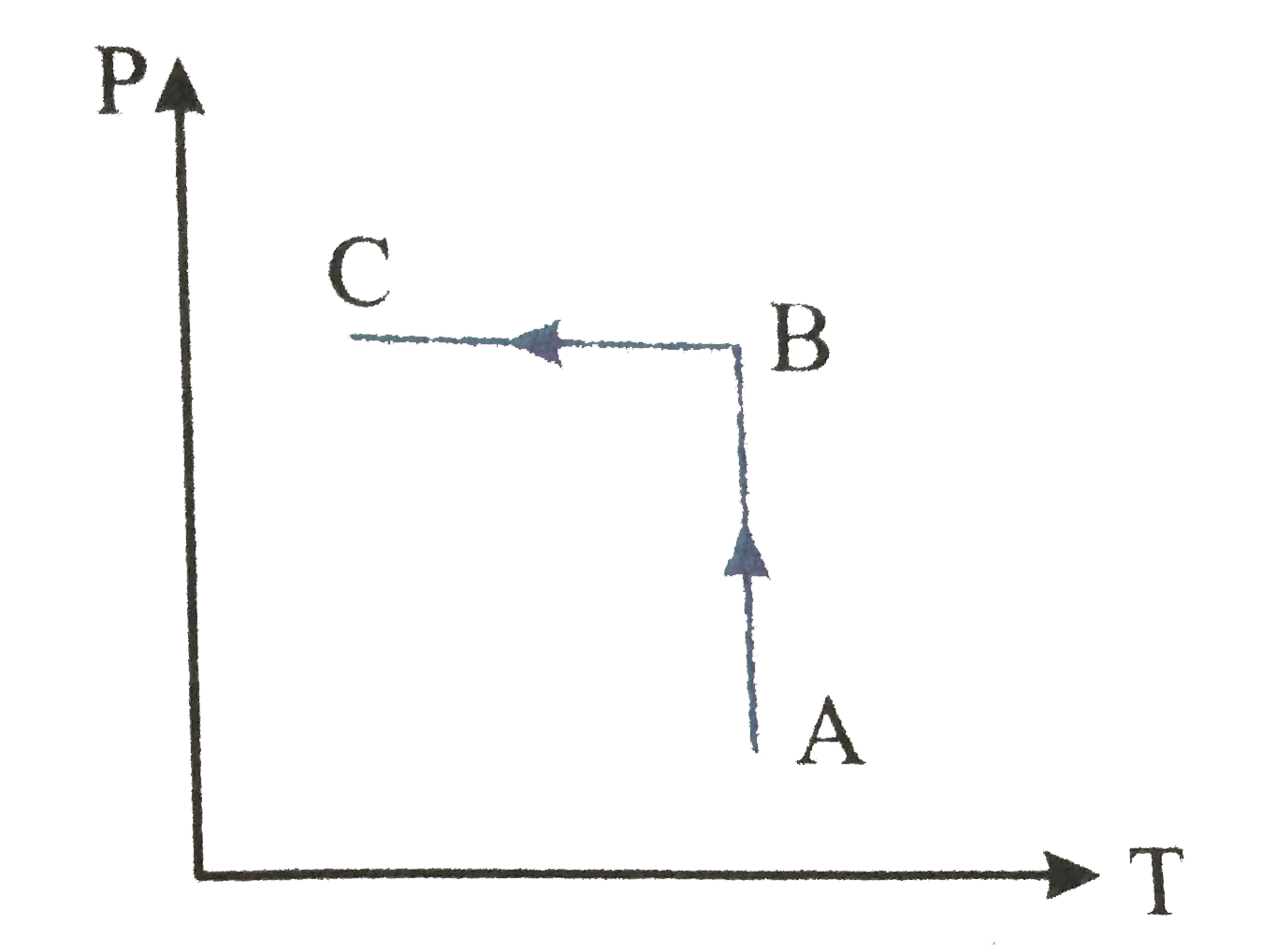 Ain process AB, work done by system is positiveBin process AB, heat is rejectedCin process AB, internal energy increasesDin process AB internal energy decreases and in process BC, internal energy increases.
Ain process AB, work done by system is positiveBin process AB, heat is rejectedCin process AB, internal energy increasesDin process AB internal energy decreases and in process BC, internal energy increases.
One mole of an ideal mono-atomic gas is taken round cyclic process ABCD as shown in figure below. Calculate
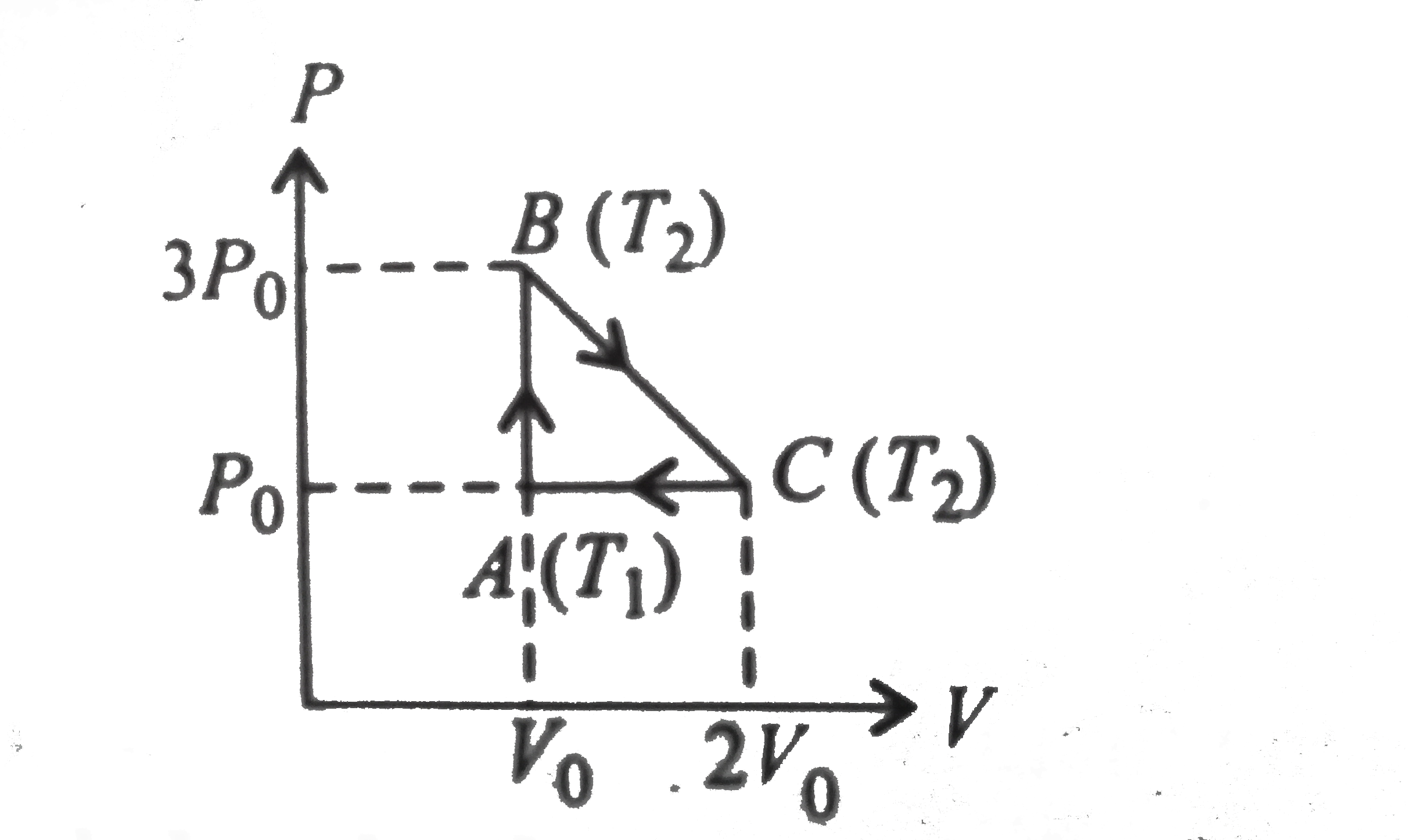 View Solution
View SolutionAn enclosed ideal gas is taken through a cycle as shown in the figure. Then
 View Solution
View SolutionAn ideal monoatomic gas is carried around the cycle ABCDA as shown in the figure. The efficiency of the gas cycle is
 View Solution
View SolutionOne mole of an ideal monoatomic gas is heated at a constant pressure of one atmosphere from0∘ to 100∘C. Then the change in the internal energy is
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure. The change in internal energy of the gas during the transition is
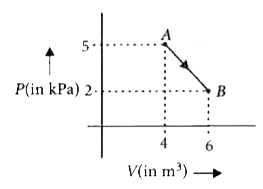 View Solution
View Solution

