How many grams of gas would be adsobed per gram of a substance at 8 atm by assuming Freundlich adsorption isotherm.
xm=kp1/n
and k=10−2atm−1/3 & n=3
The correct Answer is:xm=10−2×81/3=0.02g
Step by step video, text & image solution for How many grams of gas would be adsobed per gram of a substance at 8 atm by assuming Freundlich adsorption isotherm. x/m=kp^(1//n) and k=10^(-2) atm^(-1//3)" "&" "n=3 by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
For Freundlich adsorption isotherm, xm=kp1/n , the value of n is
Aawlays greater tham 1Balways smaller than 1Calways equal to 1Dgreater than 1 at low temperature and smaller than 1 at high temperatute - Question 2 - Select One
Freundlich adsorption isotherm x/m=kp1/n may be graphically represented as
A B
B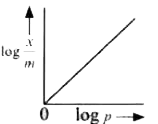 C
C D
D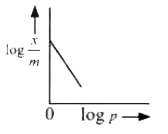
- Question 3 - Select One
Assertion (A) : Chemisorption is highly specific and occurs only when there is a possibility of chemical bond formation.
Reason (R) : Freundlich adsorption isotherm is given by the equation
xm=kp1/n(n>1)ABoth Assertion (A) and Reason (R) are correct statements, and Reason (R) is the correct explanation of the Assertion (A).BBoth Assertion (A) and Reason (R) are correct statements, but Reason (R) is not the correct explanation of the Assertion (A)CAssertion (A) is correct, but Reason (R) is incorrect statementDAssertion (A) is incorrect, but Reason (R) is correct statement.
How many grams of NH4NO3 should be dissolved per litre of solution to have a ph of 5.13 ? Kb for NH3 iss 1.8×103
View SolutionFreundlich adsorption isotherm is obeyed by the adsorption where the adsorbate forms a multimolecular layer on the surface of adsorbent .In such cases, the degree of adsorption varies linearly with pressure but at high pressure, it becomes independent of pressure
The relation of Freundlich adsorption isotherm is :
xm=kP1/n
where ,K and n are constants.
Langmuir adsorption isotherm is obeyed by the adsorption where the adsorbate forms only a unimolecular adsorbed layer. The mathematical relation of Langmuir isotherm is :
xm=aP1+bP
In the mathematical relation of Freundlich adsorption isotherm ,the value of (1/n) is 0≤1n≤1.
(a) True (b) FalseView SolutionFreundlich adsorption isotherm is obeyed by the adsorption where the adsorbate forms a multimolecular layer on the surface of adsorbent .In such cases, the degree of adsorption varies linearly with pressure but at high pressure, it becomes independent of pressure
The relation of Freundlich adsorption isotherm is :
xm=kP1/n
where ,K and n are constants.
Langmuir adsorption isotherm is obeyed by the adsorption where the adsorbate forms only a unimolecular adsorbed layer. The mathematical relation of Langmuir isotherm is :
xm=aP1+bP
Freundlich adsorption isotherm is valid for chemisorption .
(a) True (b) FalseView SolutionFreundlich adsorption isotherm is obeyed by the adsorption where the adsorbate forms a multimolecular layer on the surface of adsorbent .In such cases, the degree of adsorption varies linearly with pressure but at high pressure, it becomes independent of pressure
The relation of Freundlich adsorption isotherm is :
xm=kP1/n
where ,K and n are constants.
Langmuir adsorption isotherm is obeyed by the adsorption where the adsorbate forms only a unimolecular adsorbed layer. The mathematical relation of Langmuir isotherm is :
xm=aP1+bP
When log(xm) is plotted against log P, we get a straight line with slope (1/n).
(a) True (b) FalseView SolutionFreundlich adsorption isotherm is obeyed by the adsorption where the adsorbate forms a multimolecular layer on the surface of adsorbent .In such cases, the degree of adsorption varies linearly with pressure but at high pressure, it becomes independent of pressure
The relation of Freundlich adsorption isotherm is :
xm=kP1/n
where ,K and n are constants.
Langmuir adsorption isotherm is obeyed by the adsorption where the adsorbate forms only a unimolecular adsorbed layer. The mathematical relation of Langmuir isotherm is :
xm=aP1+bP
The degree of adsorption (x/m) at low pressure will be :
xm=a
(a) True (b) FalseView Solution

