Let AD and BC be two vertical poles at A and B respectively on a horizontal ground . If AD=8m , BC=11m and AB=10 m, then the distance ( in meters ) of a point M on AB from the point A such that MD2+MC2 is miniumu is ________________
To solve the problem, we need to find the distance of a point M on the line segment AB from point A such that the sum of the squares of the distances from M to points D and C is minimized.
1. Understanding the Geometry:
- We have two vertical poles AD and BC, where AD = 8 m and BC = 11 m.
- The distance between points A and B on the ground is AB = 10 m.
- Let M be a point on line segment AB, and let AM = x meters. Thus, MB = 10 - x meters.
2. Setting Up the Distances:
- The distance MD can be calculated using the Pythagorean theorem:
MD=√AD2+AM2=√82+x2=√64+x2
- Similarly, the distance MC is:
MC=√BC2+MB2=√112+(10−x)2=√121+(10−x)2
3. Expressing the Function to Minimize:
- We need to minimize the function:
F(x)=MD2+MC2
- Expanding this gives:
F(x)=(64+x2)+(121+(10−x)2)
- Simplifying further:
F(x)=64+x2+121+(100−20x+x2)=285+2x2−20x
4. Finding the Minimum:
- To find the minimum value of F(x), we take the derivative and set it to zero:
F′(x)=4x−20
- Setting the derivative to zero:
4x−20=0⟹4x=20⟹x=5
5. Conclusion:
- The distance of point M from point A is x=5 meters.
Final Answer:
The distance of point M from point A such that MD2+MC2 is minimized is 5 meters.
- We have two vertical poles AD and BC, where AD = 8 m and BC = 11 m.
- The distance between points A and B on the ground is AB = 10 m.
- Let M be a point on line segment AB, and let AM = x meters. Thus, MB = 10 - x meters.
- The distance MD can be calculated using the Pythagorean theorem:
MD=√AD2+AM2=√82+x2=√64+x2
- Similarly, the distance MC is:
MC=√BC2+MB2=√112+(10−x)2=√121+(10−x)2
- We need to minimize the function:
F(x)=MD2+MC2
- Expanding this gives:
F(x)=(64+x2)+(121+(10−x)2)
- Simplifying further:
F(x)=64+x2+121+(100−20x+x2)=285+2x2−20x
- To find the minimum value of F(x), we take the derivative and set it to zero:
F′(x)=4x−20
- Setting the derivative to zero:
4x−20=0⟹4x=20⟹x=5
- The distance of point M from point A is x=5 meters.
The distance of point M from point A such that MD2+MC2 is minimized is 5 meters.
Topper's Solved these Questions
Similar Questions
Let AP and BQ be two vertical poles at points A and B, respectively. If AP=16m,BQ=22mandAB=20m, then find the distance of a point R on AB from the point A such that RP2+RQ2is minimum.
View SolutionLet AP and BQ be two vertical poles at points A and B respectively. If AP=16m, BQ=22m and AB=20m , then find the distance of a point R on AB from the point A such that RP2+RQ2 is minimum.
View Solution
Knowledge Check
L and M are the mid points of AB and BC respectively of ΔABC , right angled at B . 4LC2=
 AAB2+4BC2BBC2+4AB2CAC2+4AB2DNone of these
AAB2+4BC2BBC2+4AB2CAC2+4AB2DNone of theseLet D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
A0B0C2DNone of theseABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
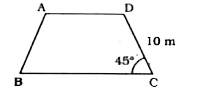 A10√2mB4√2mC5√2mD6√2m
A10√2mB4√2mC5√2mD6√2m
AB and CD are two vertical poles of heights 15 ft. and 20 ft. respectively placed at a horizontal distance of 21 ft. Find the distance of a point M form A such that the sum of the distance of M from B and D is minimum.
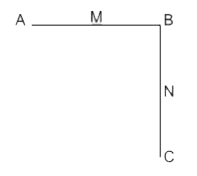
View SolutionIn the give figure AB = BC, M is the mid point of AB and N is the mid point of BC, Show that AM = NC
View SolutionTwo poles standing on a horizontal ground are of heights 5 m and 10 m respectively. The line joining their tops makes an angle of 15∘ with the ground. Let d be the distance (in m) between their poles, then (2−√3)d = ______________
View SolutionIn ΔABC, if D is any point on the side BC, show that (AB+BC+AC)>2AD.

View SolutionTwo poles standing on a horizontal ground are of heights 5 m and 10 m, respectively. The line joining their tops makes an angle of 15∘ with the ground. Then, the distance (in m) between the poles, is
View Solution
