If the mean and the standard deviation of the data 3,5,7,a,b are 5 and 2 respectively, then a and b are the roots of the equation :
x2−10x+18=0
2x2−20x+19=0
x2−10x+19=0
x2−20x+18=0
To solve the problem, we need to find the values of a and b given that the mean and standard deviation of the data set 3,5,7,a,b are 5 and 2 respectively. We will then use these values to form a quadratic equation whose roots are a and b.
1. Calculate the Mean:
The mean ¯x is given by the formula:
¯x=3+5+7+a+b5
We know the mean is 5:
3+5+7+a+b5=5
Simplifying this:
3+5+7+a+b=25
15+a+b=25
a+b=10(Equation 1)
2. Calculate the Standard Deviation:
The standard deviation σ is given by the formula:
σ=√∑(x2i)n−¯x2
Here, n=5 and σ=2:
2=√32+52+72+a2+b25−52
Squaring both sides:
4=9+25+49+a2+b25−25
4+25=9+25+49+a2+b25
29=83+a2+b25
Multiplying both sides by 5:
145=83+a2+b2
a2+b2=145−83=62(Equation 2)
3. Use Equations 1 and 2:
We have two equations:
- a+b=10 (Equation 1)
- a2+b2=62 (Equation 2)
We can use the identity:
(a+b)2=a2+b2+2ab
Substituting the known values:
102=62+2ab
100=62+2ab
2ab=100−62=38
ab=19(Equation 3)
4. Form the Quadratic Equation:
The roots of the quadratic equation can be expressed as:
x2−(a+b)x+ab=0
Substituting the values from Equations 1 and 3:
x2−10x+19=0
Final Answer:
The equation whose roots are a and b is:
x2−10x+19=0
The mean ¯x is given by the formula:
¯x=3+5+7+a+b5
We know the mean is 5:
3+5+7+a+b5=5
Simplifying this:
3+5+7+a+b=25
15+a+b=25
a+b=10(Equation 1)
The standard deviation σ is given by the formula:
σ=√∑(x2i)n−¯x2
Here, n=5 and σ=2:
2=√32+52+72+a2+b25−52
Squaring both sides:
4=9+25+49+a2+b25−25
4+25=9+25+49+a2+b25
29=83+a2+b25
Multiplying both sides by 5:
145=83+a2+b2
a2+b2=145−83=62(Equation 2)
We have two equations:
- a+b=10 (Equation 1)
- a2+b2=62 (Equation 2)
(a+b)2=a2+b2+2ab
Substituting the known values:
102=62+2ab
100=62+2ab
2ab=100−62=38
ab=19(Equation 3)
The roots of the quadratic equation can be expressed as:
x2−(a+b)x+ab=0
Substituting the values from Equations 1 and 3:
x2−10x+19=0
The equation whose roots are a and b is:
x2−10x+19=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the mean and standard deviation of 5,3,7,a,b are 5 and 2 respectively, then a and b are roots of equation.
Ax2−10x+18=0Bx2−20x+18=0Cx2−20x+19=0Dx2−10x+19=0The standard deviation for the data 7,9,11,13,15, is
A2.4B2.5C2.7D2.82The standard deviation for the data 7, 11, 15 is
A2.4B2.5C2.7D3.26
The mean and standard deviation of 1,2,3,4,5,6 are
View SolutionThe mean and the standard deviation of a data of 8 items are 25 and 5 respectively. If two terms 15 and 25 are added to this data, then the variance of the new data is
View SolutionCalculate mean and standard deviation from the following data:
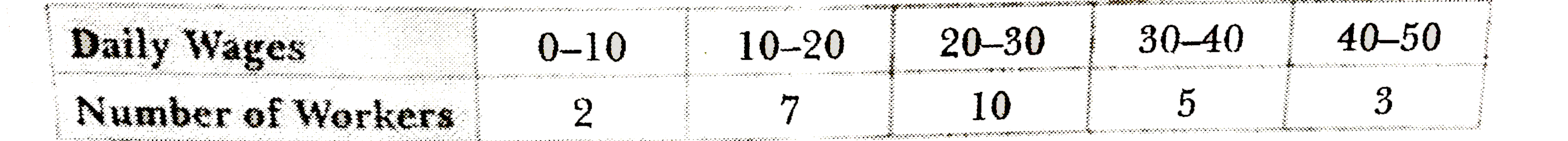
View SolutionThe standard deviation of data 6,5,9,13,12,8 and 10 is
View SolutionThe standard deviation of 5 scores 1, 2, 3, 4, 5 is
View Solution
