Among the following compounds geometrical isomerism is exhibited by :
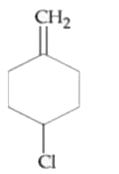
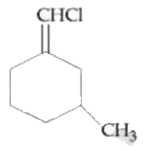
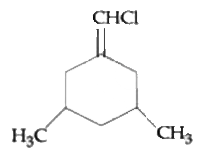
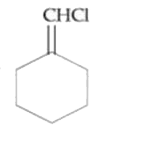
To determine which of the given compounds exhibits geometrical isomerism, we need to follow a systematic approach based on the conditions required for geometrical isomerism to occur.
1. Understanding Geometrical Isomerism:
- Geometrical isomerism occurs when there is restricted rotation around a bond, typically a double bond or in a cyclic structure.
2. Identifying the Conditions:
- Condition 1: There must be a restricted bond (double bond or ring structure).
- Condition 2: The carbon atoms involved in the restricted bond must have two different groups attached to them.
3. Analyzing Each Compound:
- Option 1: Check for restricted rotation and different groups.
- This compound has a double bond or is in a ring, and the two carbons involved have different substituents. Thus, it meets both conditions.
- Option 2: Check for restricted rotation and different groups.
- This compound also has a double bond or is in a ring, but the substituents on the involved carbons are not different enough to satisfy the second condition.
- Option 3: Check for restricted rotation and different groups.
- This compound has a double bond or is in a ring, but the two substituents on one of the carbons are identical, failing the second condition.
- Option 4: Check for restricted rotation and different groups.
- This compound has a double bond or is in a ring, but again, the substituents on one of the carbons are symmetrical, failing the second condition.
4. Conclusion:
- After analyzing all options, only Option 1 satisfies both conditions for geometrical isomerism. Therefore, it is the compound that exhibits geometrical isomerism.
Final Answer:
Option 1 is the compound that exhibits geometrical isomerism.
- Geometrical isomerism occurs when there is restricted rotation around a bond, typically a double bond or in a cyclic structure.
- Condition 1: There must be a restricted bond (double bond or ring structure).
- Condition 2: The carbon atoms involved in the restricted bond must have two different groups attached to them.
- Option 1: Check for restricted rotation and different groups.
- This compound has a double bond or is in a ring, and the two carbons involved have different substituents. Thus, it meets both conditions.
- Option 2: Check for restricted rotation and different groups.
- This compound also has a double bond or is in a ring, but the substituents on the involved carbons are not different enough to satisfy the second condition.
- Option 3: Check for restricted rotation and different groups.
- This compound has a double bond or is in a ring, but the two substituents on one of the carbons are identical, failing the second condition.
- Option 4: Check for restricted rotation and different groups.
- This compound has a double bond or is in a ring, but again, the substituents on one of the carbons are symmetrical, failing the second condition.
- After analyzing all options, only Option 1 satisfies both conditions for geometrical isomerism. Therefore, it is the compound that exhibits geometrical isomerism.
Option 1 is the compound that exhibits geometrical isomerism.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The geometrical isomerism is exhibited by
A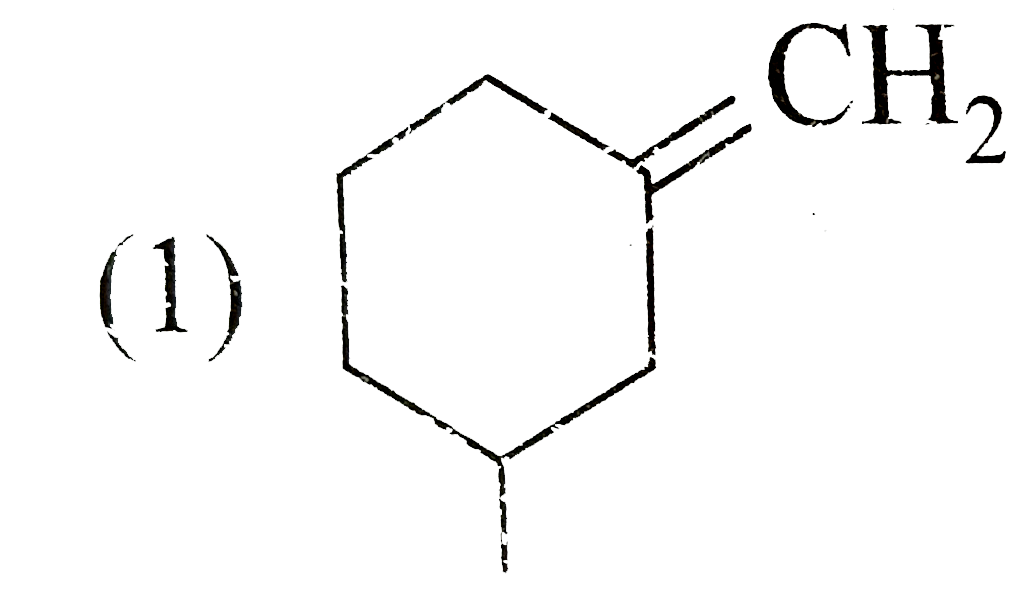 B
B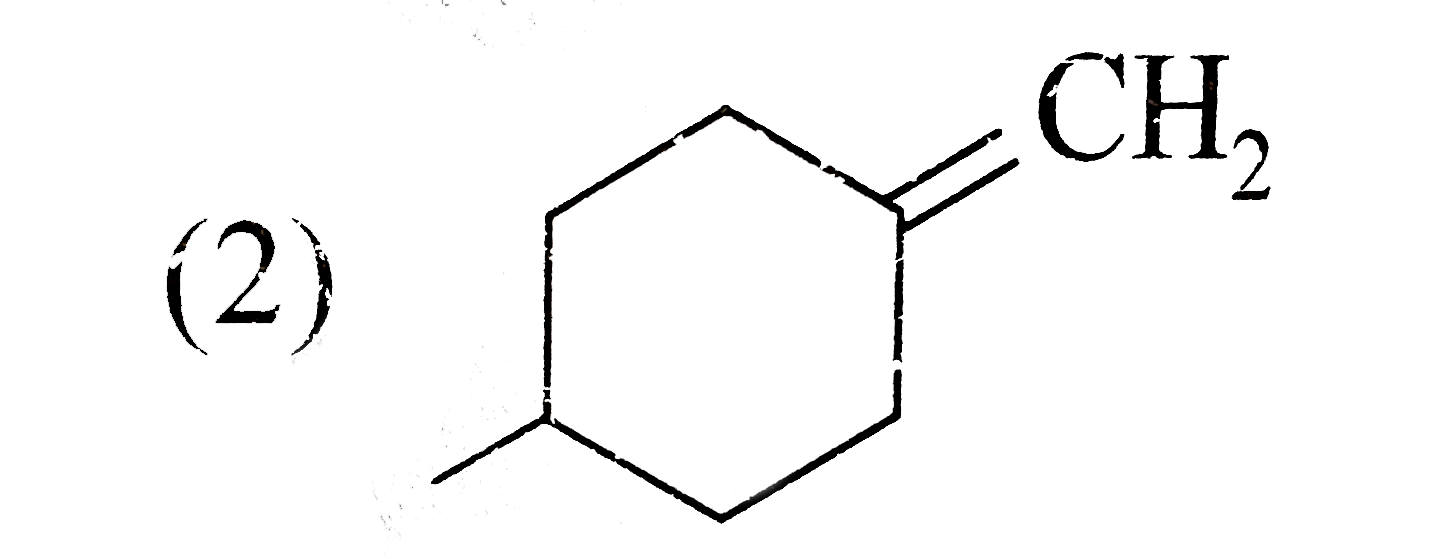 C
C D
D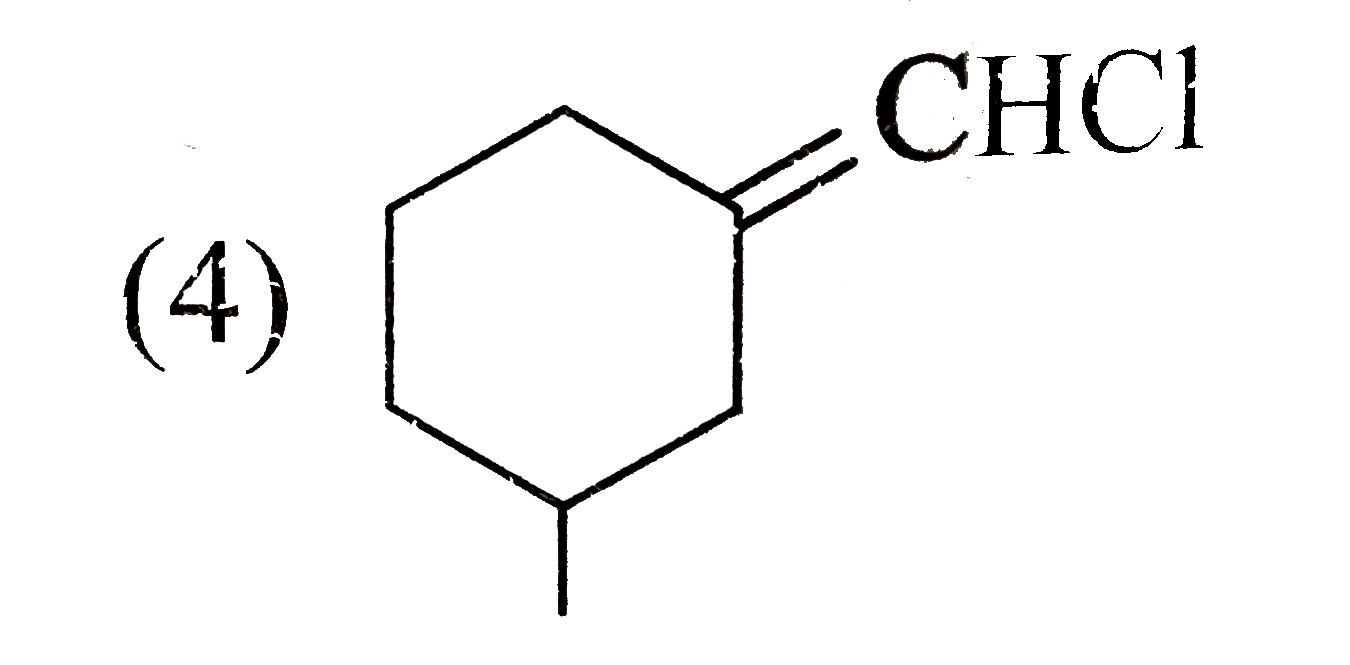
Among the following compounds which exhibits optical isomerism
APropanolB2-PropanolC1-ButanolD2-ButanolOne among the following will not show geometrical isomerism
A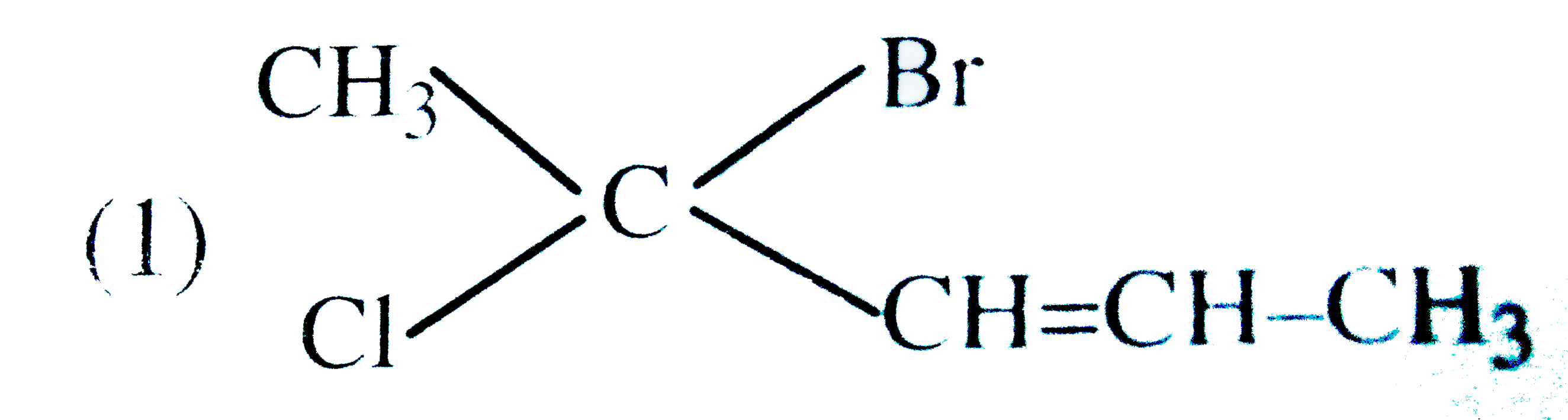 B
B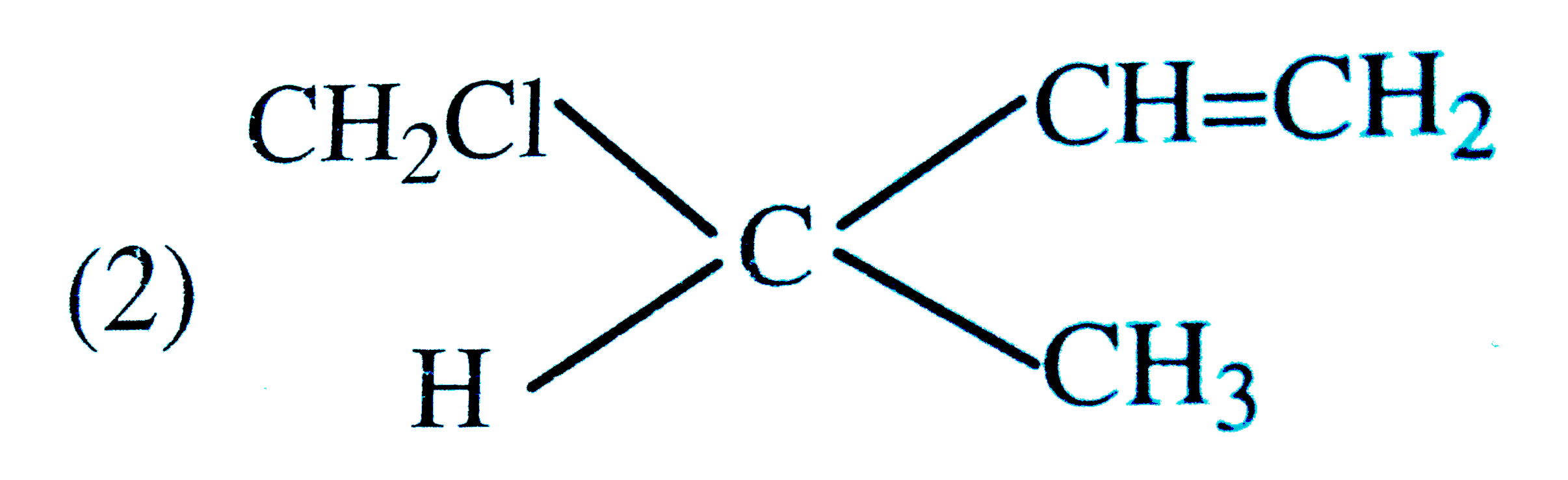 C
C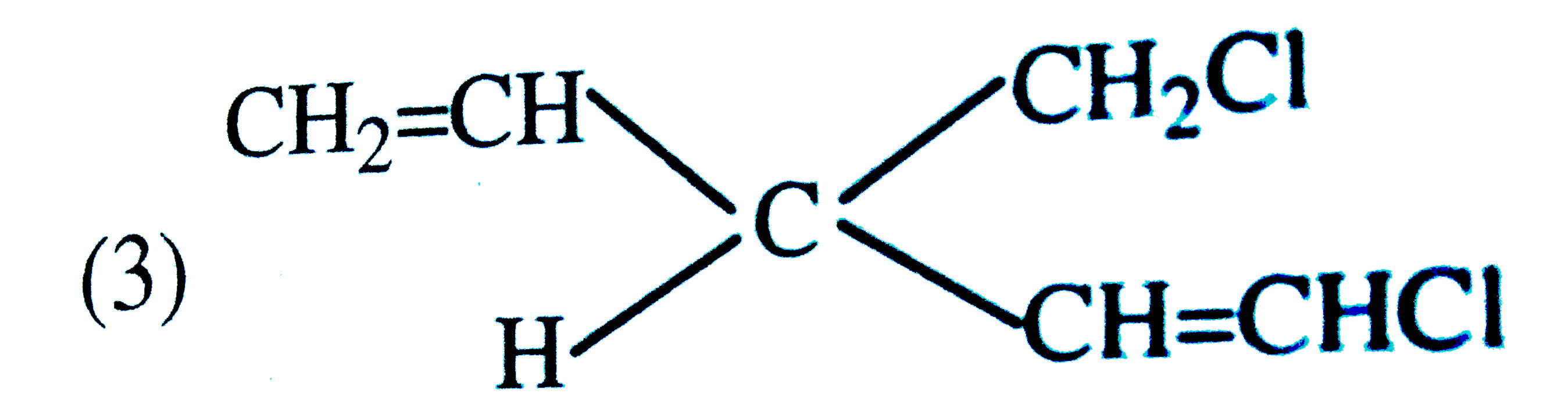 DCH3CH=CHCH2CH3
DCH3CH=CHCH2CH3
Which of the following compound can show geometrical isomerism ?
View SolutionWhich of the following compounds exhibits geometrical isomerism ?
View SolutionWhich of the following exhibits geometrical isomerism ?
View SolutionWhich of the following exhibit geometrical isomerism
View SolutionWhich of the following compound will show geometrical isomerism?
View Solution
