A pendulum of length l = 1m is released from θ0=60∘. The rate of change of speed of the bob at θ=30∘ is (g=10m/s2)
5√3m/s2
5m/s2
10m/s2
2.5m/s2
The correct Answer is:B
To find the rate of change of speed of the bob at an angle of θ=30∘, we need to calculate the tangential acceleration of the pendulum bob at that angle. Here’s the step-by-step solution:
Step 1: Identify the forces acting on the bob
When the pendulum bob is at an angle θ, the forces acting on it are:
- The gravitational force mg acting downwards.
- The tension in the string, which acts along the string.
Step 2: Break down the gravitational force
The gravitational force can be resolved into two components:
1. A component along the direction of the string: mgcosθ
2. A component perpendicular to the string (along the tangent to the path of motion): mgsinθ
Step 3: Calculate the tangential force
At θ=30∘:
- The tangential component of the gravitational force is given by:
Ftangential=mgsin(30∘)
- Since sin(30∘)=12, we can simplify this to:
Ftangential=mg⋅12=mg2
Step 4: Calculate the tangential acceleration
Using Newton's second law, the tangential acceleration at can be found using:
F=ma⟹at=Ftangentialm
Substituting the expression for the tangential force:
at=mg2m=g2
Step 5: Substitute the value of g
Given g=10m/s2:
at=102=5m/s2
Conclusion
The rate of change of speed of the bob at θ=30∘ is 5m/s2.
---
When the pendulum bob is at an angle θ, the forces acting on it are:
- The gravitational force mg acting downwards.
- The tension in the string, which acts along the string.
The gravitational force can be resolved into two components:
1. A component along the direction of the string: mgcosθ
2. A component perpendicular to the string (along the tangent to the path of motion): mgsinθ
At θ=30∘:
- The tangential component of the gravitational force is given by:
Ftangential=mgsin(30∘)
- Since sin(30∘)=12, we can simplify this to:
Ftangential=mg⋅12=mg2
Using Newton's second law, the tangential acceleration at can be found using:
F=ma⟹at=Ftangentialm
Substituting the expression for the tangential force:
at=mg2m=g2
Given g=10m/s2:
at=102=5m/s2
The rate of change of speed of the bob at θ=30∘ is 5m/s2.
Topper's Solved these Questions
Similar Questions
A pendulum bob of mass m and length L is released from angle θ with the vertical. Find
(a) the speed of the bob at the bottom of the swing and
(b) tension in the string at that time
View SolutionThe figure shows a pendulum of length l suspended at a distance x vertically above a peg.
(a) The pendulum bob is deflected through an angle θ and then released. Find the speed of the bob at the instant
(b) The pendulum is released when θ=90∘. For what x (position of peg) will the pendulum complete the circle ?
(c) The pendulum is released when θ=60∘. what is the velocity of the bob as it passes position E.

View Solution
Knowledge Check
A pendulum of length = 1 m is released from 0 = 60º. The rate of change of speed of the bob at = 30º is: (g = 10 m/s2)
 A5√3m/s2B5m/s2C10m/s2D2.5m/s2
A5√3m/s2B5m/s2C10m/s2D2.5m/s2A pendulum of mass 1 kg and length = 1m is released from rest at angle = 60º. The power delivered by all the forces acting on the bob at angle = 30º will be: (g = 10 m/s2)
A13.4WB20.4WC24.6WDzeroA simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
Amgl(1−cosθ)BmglcosθCmglsinθDNone of these
The pendulum bob B of mass M is released from rest when θ=0∘. Determine the intitial tension in the cord and also at the instant the bob reaches point D,θ=θ1. Neglect the size of the bob. Give M=3kg,θ1=45∘,L=2m,g=9.81m/s2.
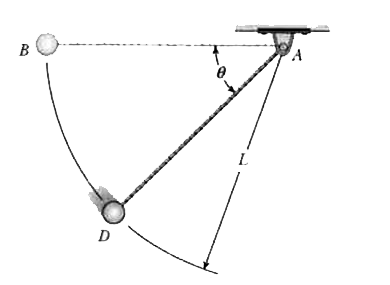
View SolutionA pendulum bob on a 2 m string is displaced 60∘ from the verticle and then released . What is the speed of the bob as it passes through the lowest point in its path?
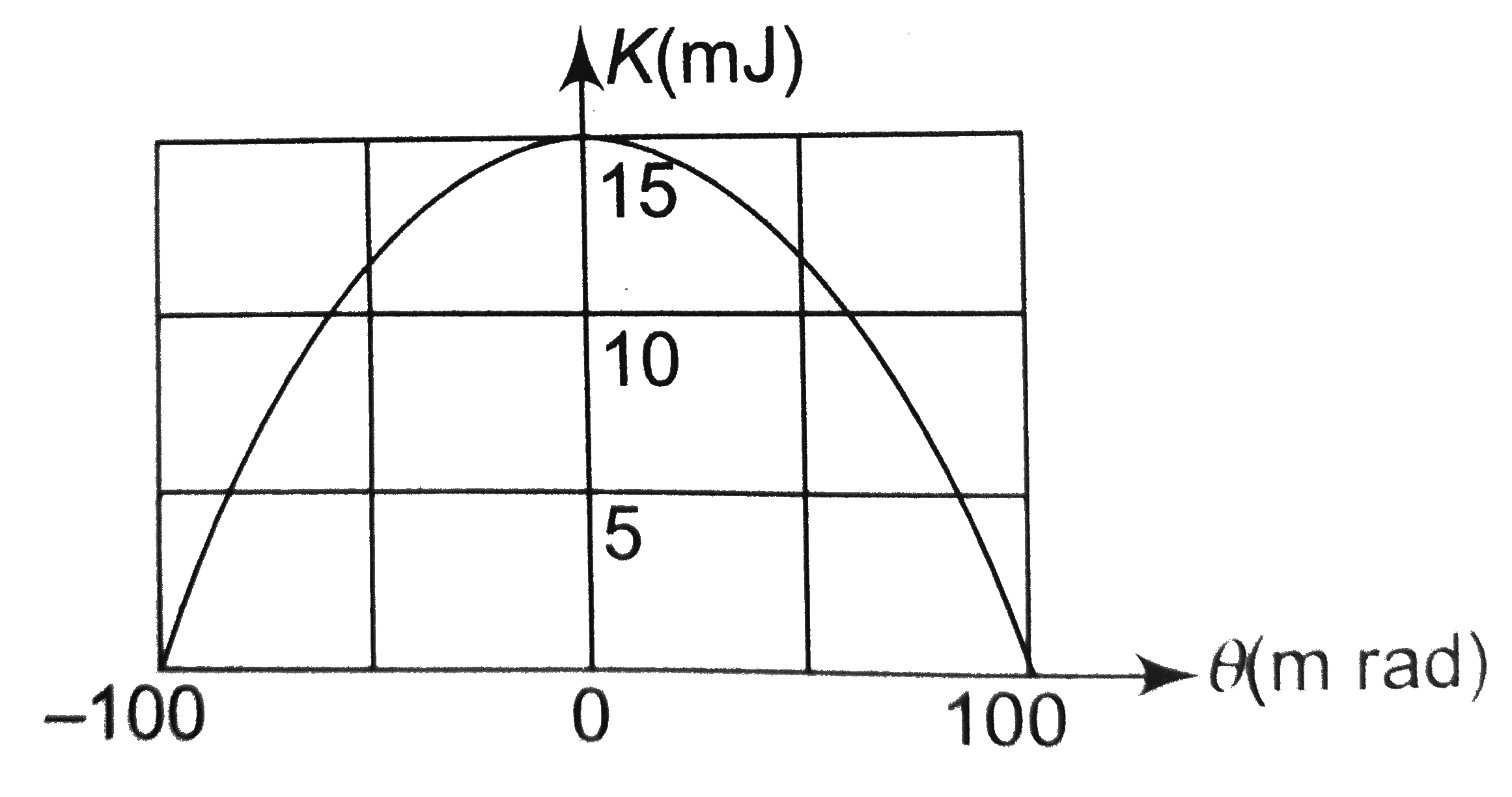
View SolutionFigure shown the kinetic energy K of a pendulum versus. its angle θ from the verticle. The pendulum bob has mass 0.2kg .The length of the pendulum is equal to (g=10m/s2)
,
View SolutionA simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
View SolutionA pendulum bob on a 2 m string is displaced 60∘ from the vertical and then released. What is the speed of the bob as it passes through the lowest point in its path
View Solution
