Neon gas of a given mass expands isothermally to double volume . What should be the further fractional decreases in pressure , so that the gas when adiabatically compressed from that state , reaches the original state ?
1−2−2/3
1−31/3
21/3
32/3
The correct Answer is:A
To solve the problem step by step, we will analyze the isothermal expansion and the subsequent adiabatic compression of the neon gas.
Step 1: Understanding the Isothermal Expansion
- The neon gas expands isothermally to double its volume.
- Let the initial volume be V and the final volume after isothermal expansion be 2V.
- According to the ideal gas law, for an isothermal process, the product of pressure and volume remains constant:
P1V=P2(2V)
- From this equation, we can derive the relationship between initial pressure P1 and final pressure P2:
P2=P12
Step 2: Analyzing the Adiabatic Compression
- Now, we need to find the pressure P3 after the gas is adiabatically compressed back to its original state.
- For an adiabatic process, the relationship between pressure and volume is given by:
PVγ=constant
- For the initial state (before adiabatic compression), we have:
P2(2V)γ=P1Vγ
- Substituting P2=P12:
P12(2V)γ=P1Vγ
- Simplifying this gives:
P12⋅2γVγ=P1Vγ
- Dividing both sides by P1Vγ:
12⋅2γ=1
- This leads to:
P3=P1⋅21−γ
Step 3: Finding the Fractional Decrease in Pressure
- The fractional decrease in pressure from P2 to P3 is given by:
Fractional Decrease=P2−P3P2
- Substituting the values of P2 and P3:
Fractional Decrease=P12−P1⋅21−γP12
- Simplifying this expression:
=1−21−γ1
Step 4: Substitute the Value of γ
- For neon gas, γ=53:
Fractional Decrease=1−21−53=1−2−23
Final Answer
- The final expression for the fractional decrease in pressure is:
1−2−23
- The neon gas expands isothermally to double its volume.
- Let the initial volume be V and the final volume after isothermal expansion be 2V.
- According to the ideal gas law, for an isothermal process, the product of pressure and volume remains constant:
P1V=P2(2V)
- From this equation, we can derive the relationship between initial pressure P1 and final pressure P2:
P2=P12
- Now, we need to find the pressure P3 after the gas is adiabatically compressed back to its original state.
- For an adiabatic process, the relationship between pressure and volume is given by:
PVγ=constant
- For the initial state (before adiabatic compression), we have:
P2(2V)γ=P1Vγ
- Substituting P2=P12:
P12(2V)γ=P1Vγ
- Simplifying this gives:
P12⋅2γVγ=P1Vγ
- Dividing both sides by P1Vγ:
12⋅2γ=1
- This leads to:
P3=P1⋅21−γ
- The fractional decrease in pressure from P2 to P3 is given by:
Fractional Decrease=P2−P3P2
- Substituting the values of P2 and P3:
Fractional Decrease=P12−P1⋅21−γP12
- Simplifying this expression:
=1−21−γ1
- For neon gas, γ=53:
Fractional Decrease=1−21−53=1−2−23
- The final expression for the fractional decrease in pressure is:
1−2−23
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTECHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -C) (Previous Year Questions)
54 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTECHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTECHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -A) (Objective Type Questions)
39 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTECHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-J) Akash Challengers Questions
7 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTECHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
Knowledge Check
The correct figure representing isothermal and adiabatic compression of an ideal gas from the same initial state is:
A B
B C
C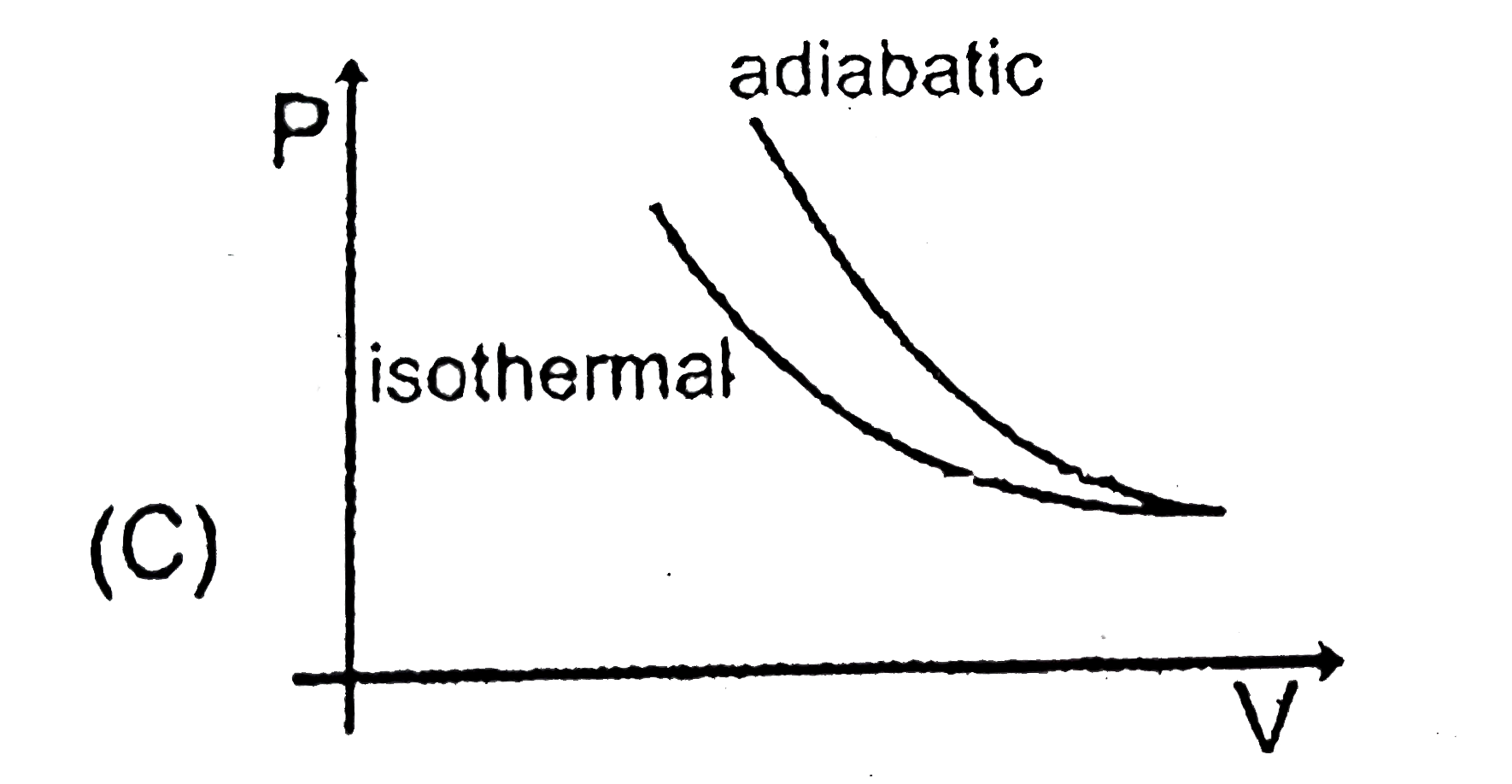 D
D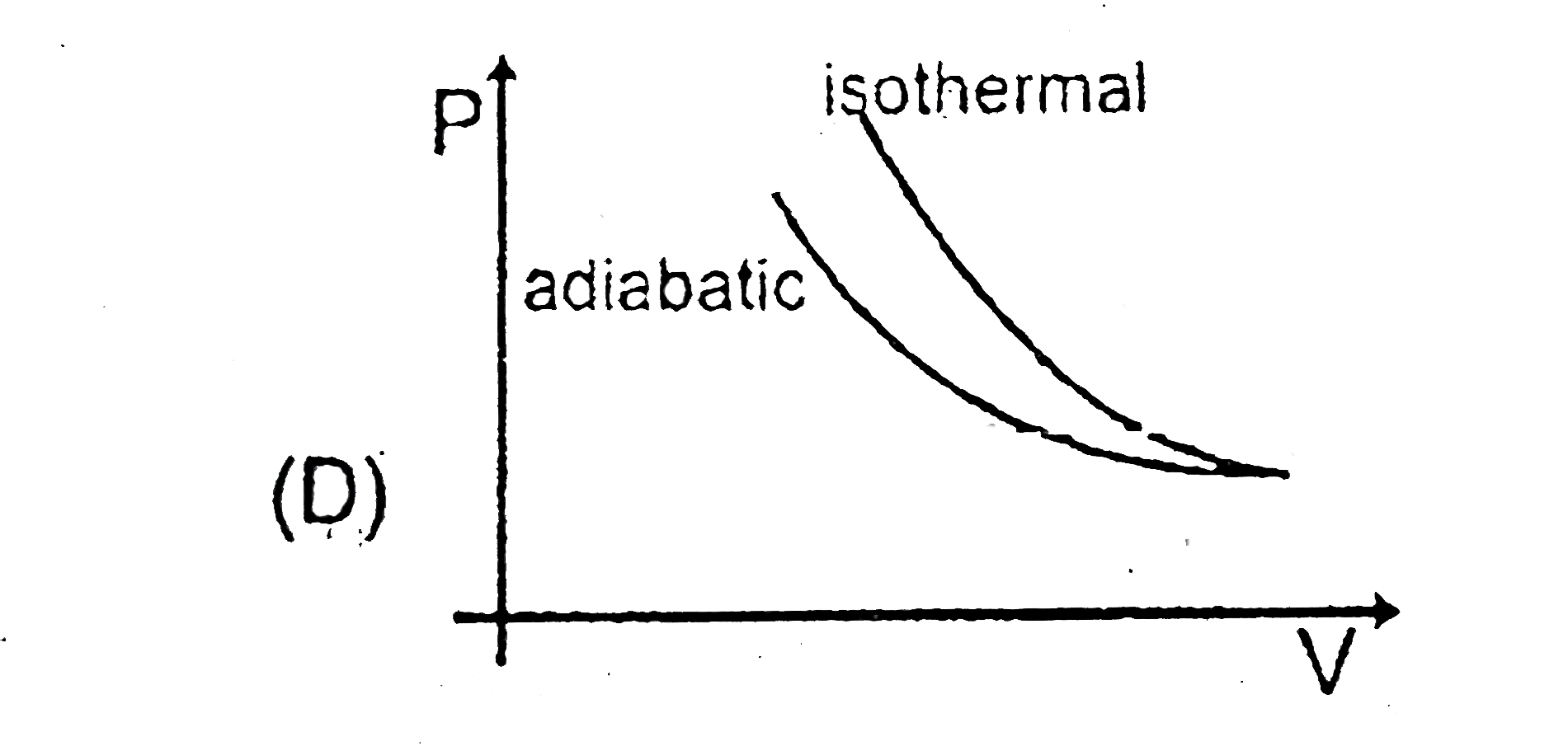
A gas is compressed adiabatically to half its volume. By what factor does the pressure of the gas increase?
A2B2.64C1.4D2.4A mass of gas is first expanded isothermally and then compressed adiabatically to its original volume. What further simplest operation must be performed on the gas to restore it to its original state?
AAn isobaric cooling to bring its temperature to initial valueBAn isochoric cooling to bring its pressure to its initial valueCAn isothermal process to take its pressure to its initial valueDAn isochoric heating to bring its temperature to initial value
An ideal gas with pressure P, volume V and temperature T is expanded isothermically to a volume 2V and a final pressure Pi, If the same gas is expanded adiabatically to a volume 2V, the final pressure Pa. The ratio of the specific heats of the gas is 1.67. The ratio PaP1 is .......
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and final pressure PI. The same gas is expanded adiabatically to a volume 2V and final pressure in this case is PA. In terms of the ratio of the two specific heats for the gas γ, the ratio PI/PA is
View SolutionAn ideal gas of volume V and pressure P expands isothermally to volume 16 V and then compressed adiabatically to volume V . The final pressure of gas is [γ=1.5]
View SolutionOne mole of an ideal gas at pressure P0 and temperature T0 is expanded isothermally to twice ist volume and then compressed at constant pressure to (V0/2) and the gas is brought bac to original state by a process in which PαV (pressure is direclty proportional to volume). The correct temperature of the process is
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and final pressure PI. The same gas is expanded adiabatically to a volume 2V and final pressure in this case is PA. In terms of the ratio of the two specific heats for the gas γ, the ratio PI/PA is
View Solution
