An observer is approaching with a speed v , towards a stationary source emitting sound waves of wavelength λ0 . The wavelength shift detected by the observer is ( Take c= speed of sound )
λ0vc
λ0cv
λ0v2c2
Zero
The correct Answer is:D
To solve the problem of finding the wavelength shift detected by an observer approaching a stationary sound source, we can follow these steps:
1. Understanding the Setup:
- We have a stationary sound source emitting sound waves with a wavelength λ0.
- An observer is moving towards the source with a speed v.
- The speed of sound in the medium is denoted as c.
2. Using the Doppler Effect:
- The Doppler effect describes how the frequency of a wave changes for an observer moving relative to the source of the wave.
- The formula for the observed frequency f′ when the observer is moving towards a stationary source is given by:
f′=fs(c+vc)
where fs is the frequency emitted by the source.
3. Relating Frequency and Wavelength:
- The frequency of a wave is related to its wavelength by the equation:
f=cλ
- Therefore, we can express the emitted frequency fs in terms of the wavelength λ0:
fs=cλ0
4. Substituting into the Doppler Effect Formula:
- Substitute fs into the observed frequency equation:
f′=cλ0(c+vc)=c+vλ0
5. Finding the Observed Wavelength:
- Now, we can find the observed wavelength λ using the relationship between frequency and wavelength:
f′=cλ
- Setting the two expressions for f′ equal gives:
c+vλ0=cλ
6. Rearranging for the Observed Wavelength:
- Rearranging the equation to solve for λ:
λ=cλ0c+v
7. Calculating the Wavelength Shift:
- The wavelength shift Δλ is defined as the difference between the emitted wavelength λ0 and the observed wavelength λ:
Δλ=λ0−λ
- Substituting the expression for λ:
Δλ=λ0−cλ0c+v
- Factoring out λ0:
Δλ=λ0(1−cc+v)
- Simplifying the expression:
Δλ=λ0((c+v)−cc+v)=λ0(vc+v)
Final Result:
Thus, the wavelength shift detected by the observer is:
Δλ=vλ0c+v
- We have a stationary sound source emitting sound waves with a wavelength λ0.
- An observer is moving towards the source with a speed v.
- The speed of sound in the medium is denoted as c.
- The Doppler effect describes how the frequency of a wave changes for an observer moving relative to the source of the wave.
- The formula for the observed frequency f′ when the observer is moving towards a stationary source is given by:
f′=fs(c+vc)
where fs is the frequency emitted by the source.
- The frequency of a wave is related to its wavelength by the equation:
f=cλ
- Therefore, we can express the emitted frequency fs in terms of the wavelength λ0:
fs=cλ0
- Substitute fs into the observed frequency equation:
f′=cλ0(c+vc)=c+vλ0
- Now, we can find the observed wavelength λ using the relationship between frequency and wavelength:
f′=cλ
- Setting the two expressions for f′ equal gives:
c+vλ0=cλ
- Rearranging the equation to solve for λ:
λ=cλ0c+v
- The wavelength shift Δλ is defined as the difference between the emitted wavelength λ0 and the observed wavelength λ:
Δλ=λ0−λ
- Substituting the expression for λ:
Δλ=λ0−cλ0c+v
- Factoring out λ0:
Δλ=λ0(1−cc+v)
- Simplifying the expression:
Δλ=λ0((c+v)−cc+v)=λ0(vc+v)
Thus, the wavelength shift detected by the observer is:
Δλ=vλ0c+v
Topper's Solved these Questions
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-B ( Objective type Questions ))
42 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-C ( Previous year Questions ))
52 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - EXERCISE
19 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTECHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
15 Videos
Similar Questions
Knowledge Check
An observer is moving towards the stationary source of sound, then
AApparent frequency will be less than the real frequencyBApparent frequency will be greater than the real frequencyCApparent frequency will be equal to real frequencyDOnly the quality of sound will changeSpeed of sound wave is v. If a reflector moves towards a stationary source emitting waves of frequency f with speed u, the wavelength of reflected waves will be
Av−uv+ufBv+uvfCv+uv−ufDv−uvfAn observer approaches towards a stationary source of sound at constant velocity and recedes away at the same speed. The graph of wavelength observed with time is:
A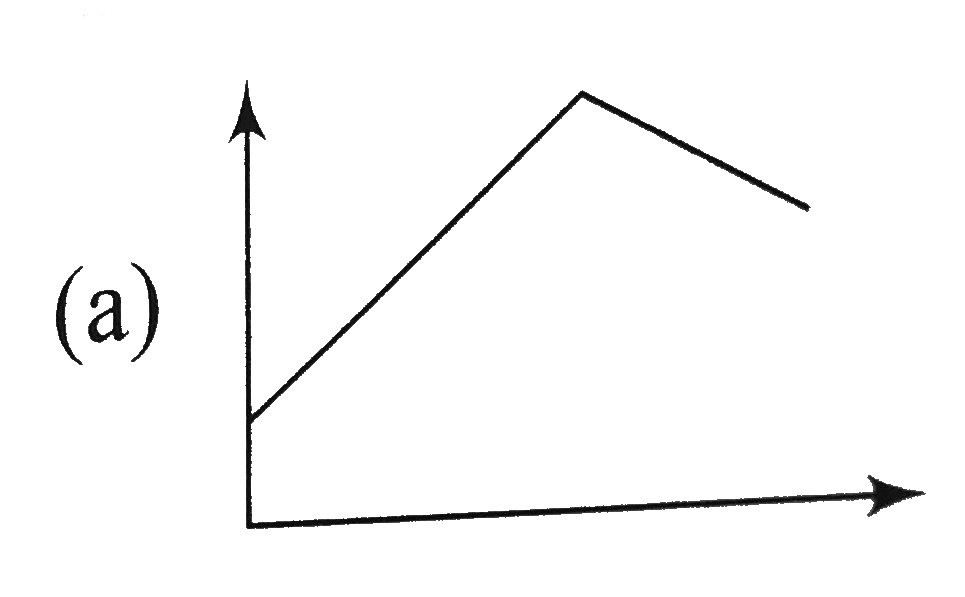 B
B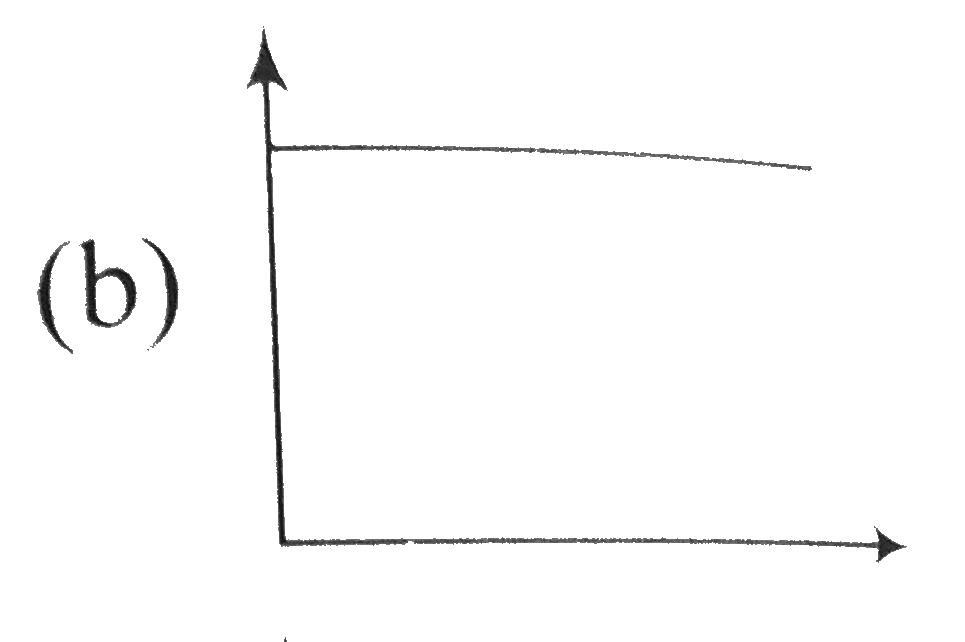 C
C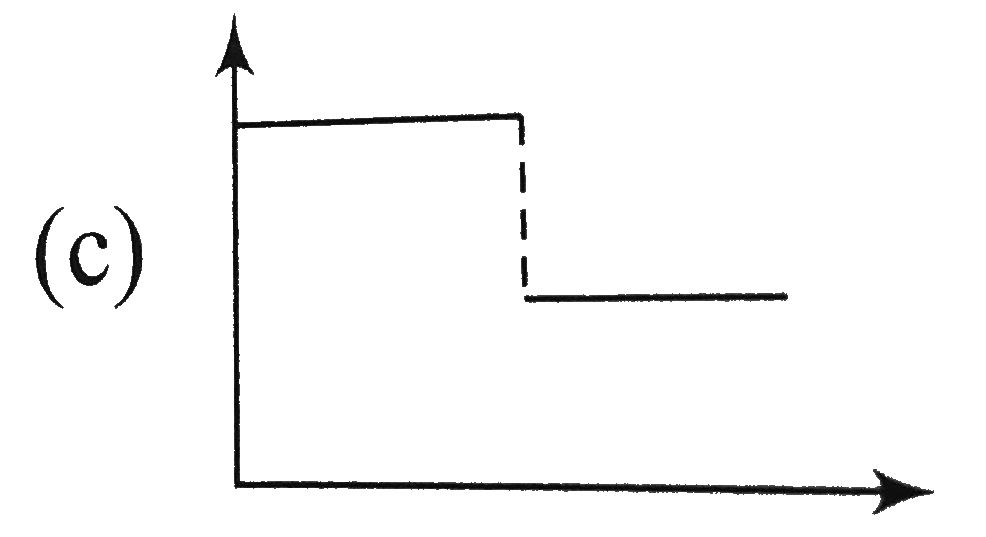 D
D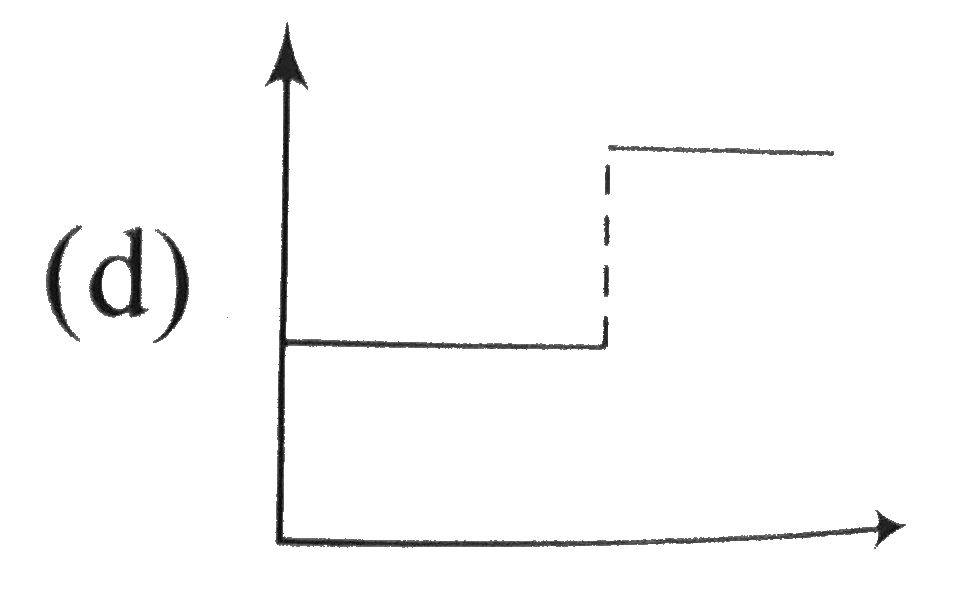
a bus is moving towards and stationary observer with speed 20 m/s blows a horn of frequency 200 Hz. the frequency of sound heard by the observer is approximately ( take speed of sound 320 m/s)
View SolutionAn observer moves towards a stationary source of sound. The percentage change in the apparent frequency is
View SolutionA source producing sound of frequency 170 Hz is approaching a stationary observer with a velocity 17ms−1. The apparent change in the wavelength of sound heard by the observer is (speed of sound in air =340ms−1)
View SolutionTwo stationary sources each emitting waves of wavelength λ , an observer moves from one source to another with velocity u. Then number of beats heard by him is
View SolutionA sound source emits sound waves of frequency 500 Hz and wavelength 0.2 m. How long does it take the waves to travel 300 m.
View Solution
