If two identical heaters each rated as (1000 W, 220V) are connected are connected in parallel to 220 V, then the total power consumed is .
500 W
2500W
250W
2000 W
To solve the problem step by step, we will follow these steps:
Step 1: Understand the given information
We have two identical heaters, each rated at 1000 W and 220 V, connected in parallel to a 220 V supply.
Step 2: Calculate the resistance of one heater
Using the formula for power:
P=V2R
We can rearrange this to find the resistance R:
R=V2P
Substituting the values:
R=(220)21000
Calculating this gives:
R=484001000=48.4Ω
Step 3: Determine the equivalent resistance of the parallel combination
For two resistors R1 and R2 in parallel, the equivalent resistance Req is given by:
1Req=1R1+1R2
Since both heaters are identical:
1Req=1R+1R=2R
Thus,
Req=R2=48.42=24.2Ω
Step 4: Calculate the total power consumed
Using the formula for power in terms of voltage and resistance:
Ptotal=V2Req
Substituting the values:
Ptotal=(220)224.2
Calculating this gives:
Ptotal=4840024.2≈2000W
Conclusion
The total power consumed by the two heaters connected in parallel is approximately 2000 W.
---
We have two identical heaters, each rated at 1000 W and 220 V, connected in parallel to a 220 V supply.
Using the formula for power:
P=V2R
We can rearrange this to find the resistance R:
R=V2P
Substituting the values:
R=(220)21000
Calculating this gives:
R=484001000=48.4Ω
For two resistors R1 and R2 in parallel, the equivalent resistance Req is given by:
1Req=1R1+1R2
Since both heaters are identical:
1Req=1R+1R=2R
Thus,
Req=R2=48.42=24.2Ω
Using the formula for power in terms of voltage and resistance:
Ptotal=V2Req
Substituting the values:
Ptotal=(220)224.2
Calculating this gives:
Ptotal=4840024.2≈2000W
The total power consumed by the two heaters connected in parallel is approximately 2000 W.
Similar Questions
Knowledge Check
If two identical heaters each rated as (1000 W, 220 V) are connected in parallel to 220 V, then the total power consumed is
A500wB2500WC250WD2000WTwo identical electric lamps marked 500W, 220V are connected in series and then joined to a 110V line. The power consumed by each lamp is
A1254WB254WC2254WD125WFour identical bulbs each rated 100 watt, 220 volts are connected across a battery as shown. The total electric power consumed by the bulbs is:
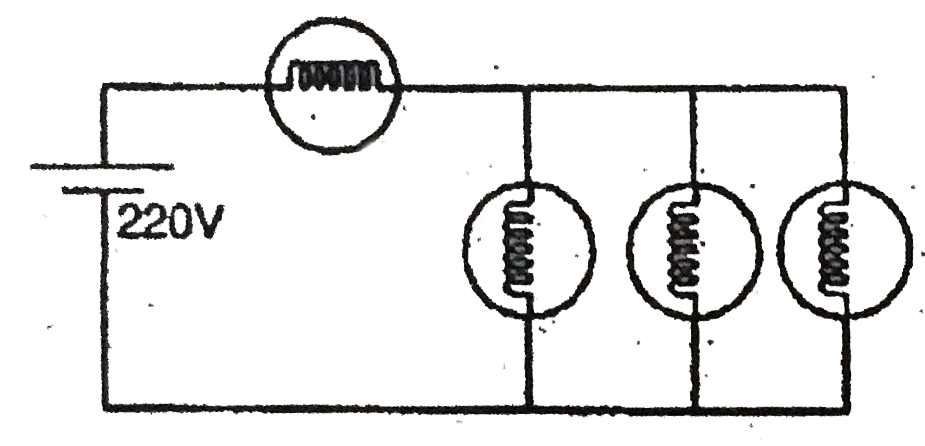 A75 wattB400 wattC300 wattD400/3 watt
A75 wattB400 wattC300 wattD400/3 watt
An electric heater and an electric bulb are rated 500W. 220V and 100W, 220V respectively. Both are connected in series to a 220V d.c. mains. Calculate the power consumed by (i) the heater ana (ii) electric bulb.
View SolutionAn electric bulb and electric heater are rated 100W,220Vand500W,220V respectively. Both are connected in series to a 220V d.c. mains. Calculate the power consumed by (i) electric bulb and (ii) heater
View SolutionTwo identical heaters rated 220V,1000W are paced in series with each other across 220V line , then the combined power is
View SolutionIf two bulbs, both of rated power 100 W at 220 V, are connected in series with a 220 V supply, the total power consumed by the bulbs will be:
View SolutionA 25 W , 220 V bulb and a 100 W , 220 V bulb are connected in parallel across a 440 V line
View Solution
