Maximum current produced by a cell of emf 10 V and internal resistance 2Ω is
10A
2A
5A
4A
To find the maximum current produced by a cell with an EMF of 10 V and an internal resistance of 2 Ω, we can follow these steps:
1. Identify the given values:
- EMF (E) = 10 V
- Internal resistance (r) = 2 Ω
2. Understand the formula for current:
The current (I) flowing through a circuit can be calculated using Ohm's law:
I=ER+r
where:
- E = EMF of the cell
- R = external resistance
- r = internal resistance of the cell
3. Determine the condition for maximum current:
To find the maximum current, we need to minimize the total resistance in the circuit. The maximum current occurs when the external resistance (R) is zero:
Imax=Er
4. Substitute the values into the formula:
Now, substituting the values of E and r into the equation:
Imax=10V2Ω=5A
5. Conclusion:
The maximum current produced by the cell is 5 A.
Final Answer:
The maximum current produced by the cell is 5 A.
---
- EMF (E) = 10 V
- Internal resistance (r) = 2 Ω
The current (I) flowing through a circuit can be calculated using Ohm's law:
I=ER+r
where:
- E = EMF of the cell
- R = external resistance
- r = internal resistance of the cell
To find the maximum current, we need to minimize the total resistance in the circuit. The maximum current occurs when the external resistance (R) is zero:
Imax=Er
Now, substituting the values of E and r into the equation:
Imax=10V2Ω=5A
The maximum current produced by the cell is 5 A.
The maximum current produced by the cell is 5 A.
Similar Questions
Knowledge Check
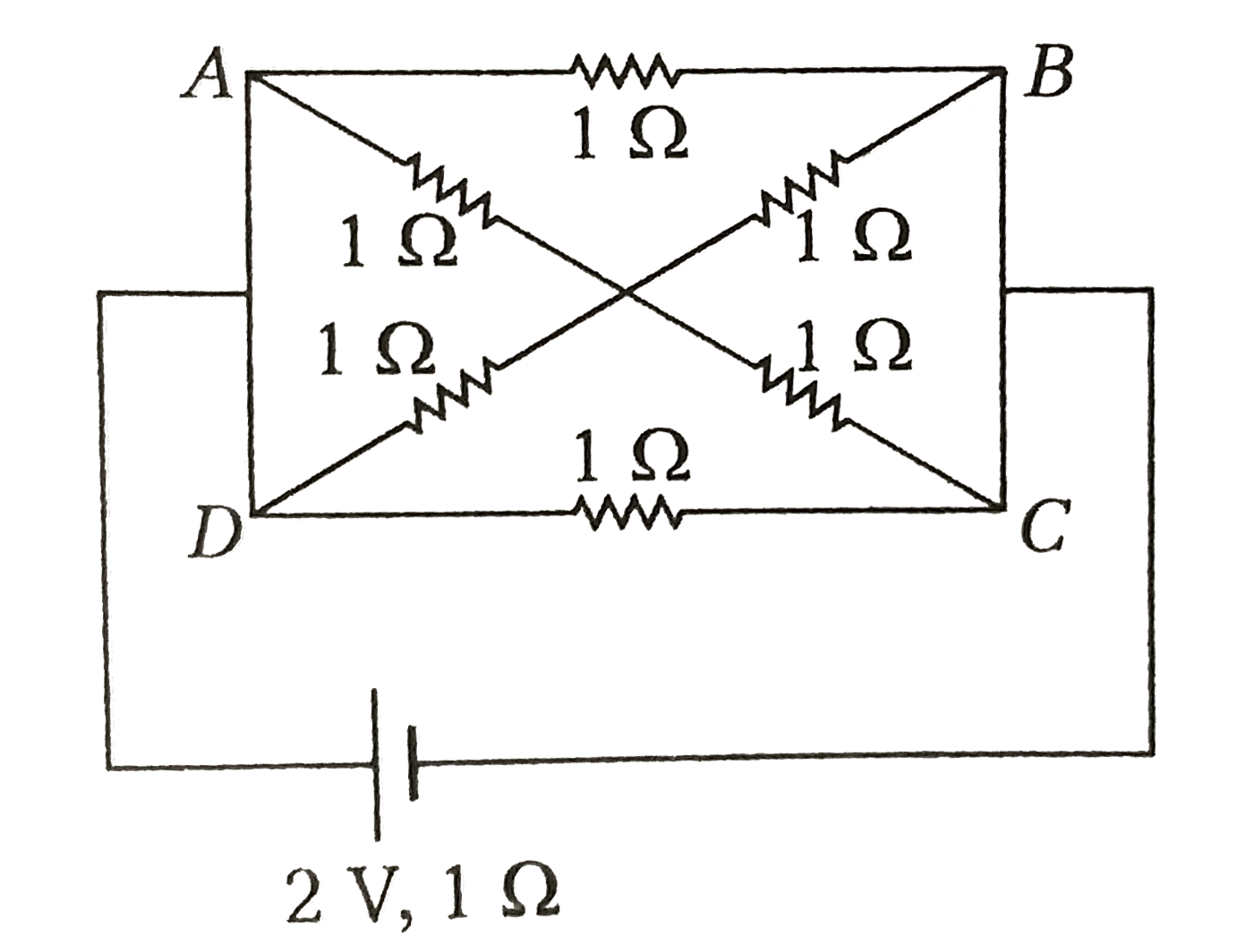
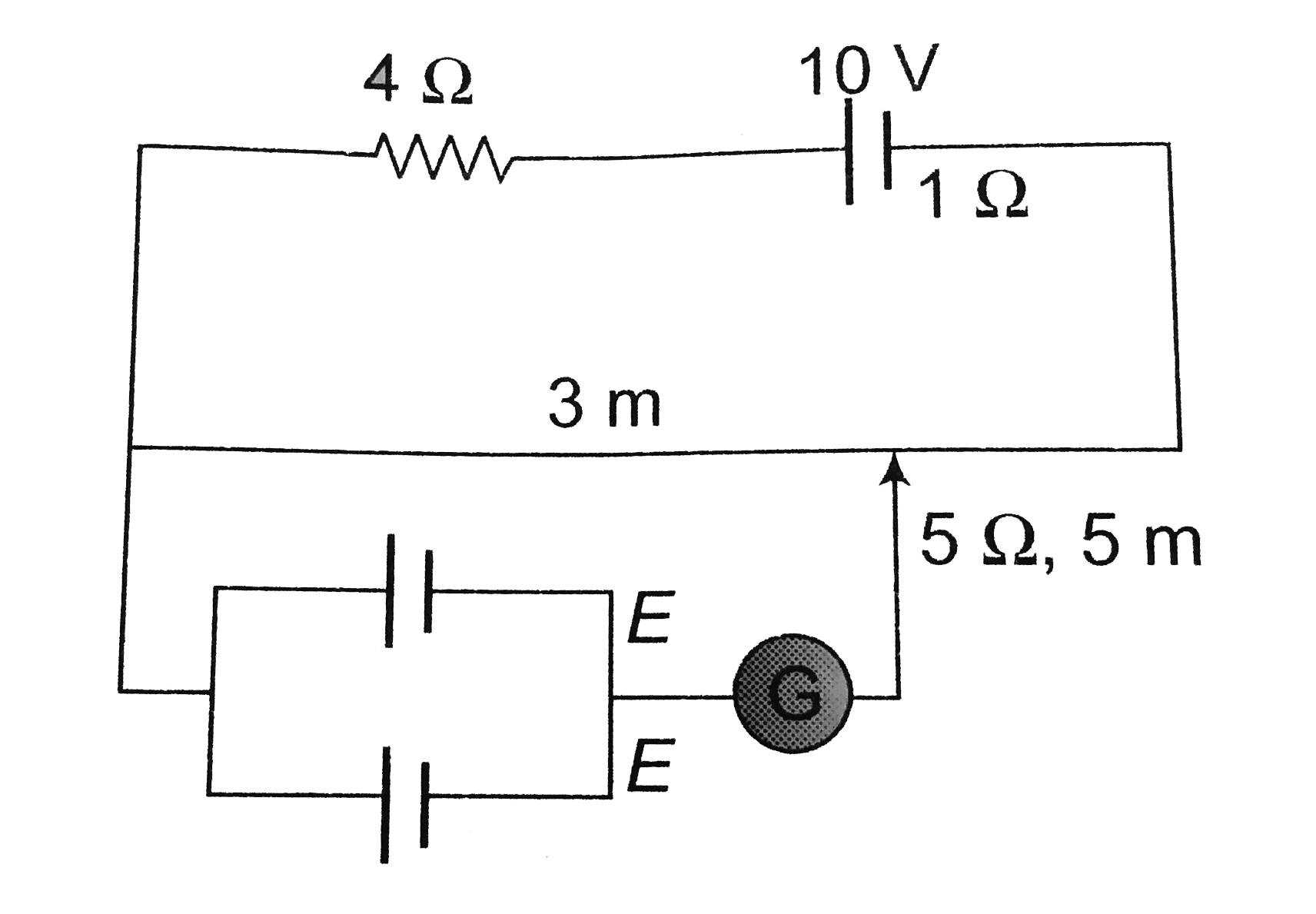
A resistance of 4Ω and a wire of length 5 meters and resistance 5Ω are joined in series and connected to a cell of e.m.f. 10V and internal resistance 1Ω. A parallel combination of two identical cells is balanced across 300cm of wire. The e.m.f. E of each cell is
 A1.5VB3.0VC0.67VD1.33V
A1.5VB3.0VC0.67VD1.33VA cell E1 of emf 6V and internal resistance 2Ω is connected with another cell E2 of emf 4V and internal resistance 8Ω (as shown in the figure). The potential difference across points X and Y is :
 A10.0 VB3.6 VC5.6VD2.0 V
A10.0 VB3.6 VC5.6VD2.0 VA voltmeter has a resistance of 50Ω is connected across a cell of e.m.f. 2V and internal resistance 10Ω. The reading of voltmeter is
A1.667VB16.7VC167VD0.167V
In a potentiometer circuit, the emf of driver cell is 2V and internal resistance is 0.5Ω. The potentiometer wire is 1m long . It is found that a cell of emf 1V and internal resistance 0.5Ω is balanced against 60 cm length of the wire. Calculate the resistance of potentiometer wire.
View SolutionA voltmeter has a resistance of 1000Ω. What will be its reading when it is connected across a cell of emf 2V and internal resistance 10Ω ?
View SolutionA resistor is connected to a battery of emf 10 V and internal resistance 0.3Ω. What is the resistance of the resistor to be inserted in the circuit for the circuit current 1.2A?
View SolutionA potentiometer wire , 4 m long and having a resistance of 10 Ω, is connected in series with an external resistance of 38Ω and a cell , of emf 2 V and internal resistance 2Ω. Calculate the potential gradient along the wire.
View SolutionA battery of emf 6V internal resistance 5Ω is joined in parallel with another cell of emf of 10V and internal resistance 1Ω and the combination is used to send current through a resistor of 12Ω. Calculate the current through each battery.
View Solution