A heater coil c onnected across a give potential difference has power P . Now , the coil is cut into two equal halves and joined in parallel . Across the same potential difference, this combination has power
P
4P
P/4
2P
The correct Answer is:A
To solve the problem step by step, we can follow these steps:
Step 1: Understand the initial power of the heater coil
The power P of the heater coil connected across a potential difference V is given by the formula:
P=V2R
where R is the resistance of the heater coil.
Step 2: Determine the resistance of the cut coil
When the coil is cut into two equal halves, the resistance of each half will be:
R′=R2
This is because resistance is directly proportional to the length of the conductor, and cutting the coil in half reduces its length by half.
Step 3: Calculate the equivalent resistance when joined in parallel
When the two halves are connected in parallel, the equivalent resistance Req can be calculated using the formula for resistances in parallel:
1Req=1R′+1R′
Substituting R′=R2:
1Req=1R2+1R2=2R/2=4R
Thus, the equivalent resistance is:
Req=R4
Step 4: Calculate the new power across the same potential difference
Now, we can find the new power P′ across the same potential difference V using the equivalent resistance:
P′=V2Req=V2R4=4V2R
Step 5: Relate the new power to the initial power
Since we know that P=V2R, we can express P′ in terms of P:
P′=4⋅V2R=4P
Final Answer
Thus, the power of the combination when the coil is cut into two halves and connected in parallel is:
P′=4P
---
The power P of the heater coil connected across a potential difference V is given by the formula:
P=V2R
where R is the resistance of the heater coil.
When the coil is cut into two equal halves, the resistance of each half will be:
R′=R2
This is because resistance is directly proportional to the length of the conductor, and cutting the coil in half reduces its length by half.
When the two halves are connected in parallel, the equivalent resistance Req can be calculated using the formula for resistances in parallel:
1Req=1R′+1R′
Substituting R′=R2:
1Req=1R2+1R2=2R/2=4R
Thus, the equivalent resistance is:
Req=R4
Now, we can find the new power P′ across the same potential difference V using the equivalent resistance:
P′=V2Req=V2R4=4V2R
Since we know that P=V2R, we can express P′ in terms of P:
P′=4⋅V2R=4P
Thus, the power of the combination when the coil is cut into two halves and connected in parallel is:
P′=4P
Similar Questions
A uniform heating wire of resistance 36 ohms is connected across a potential difference of 240 V. The wire is then cut into half and a potential difference of 240 V is applied across each half separately. The ratio of power dissipation in first case to the total power dissipation in the second case would be 1 : x, where x is _________ .
View SolutionThe power of a heating coil is P. it is cut into two equal parts. The power of one of them across same mains is
View Solution
Knowledge Check
Find the potential difference across C2.
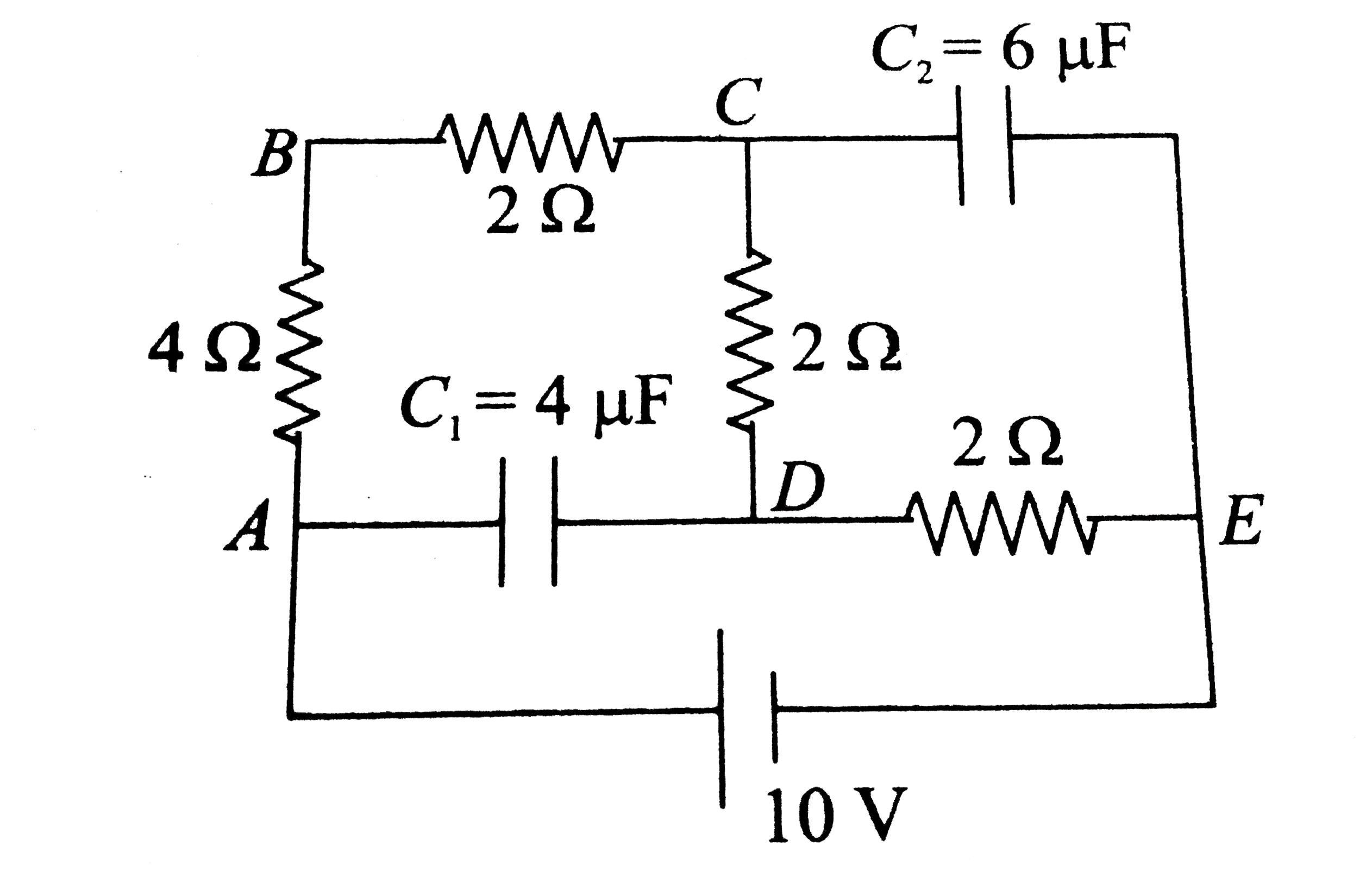 A6 VB4 VCzeroD2 V
A6 VB4 VCzeroD2 VTwo capacitors of 3μF and 6μF are connected in series and a potential difference of 900 V is applied across the combination. They are then disconnected and reconnected in parallel. The potential difference across the combination is
AZeroB100 VC200 VD400 VA heater coil is cut into two equal parts and only one part is now used in the heater. The heat generated will now be
Afour timesBdoubledChalvedDone fourth
Power generated across a uniform wire connected across a supply is H. If the wire is cut into n equal parts and all the parts are connected in parallel across the same supply, the total power generated in the wire is
View SolutionA heater coil connected to a supply of a 220 V is dissipating some power . P1 The coil is cut into half and the two halves are connected in parallel. The heater now dissipates a power . P2 Theratio of power P1:P2 is
View SolutionA heating coil is labelled 100W,220V. The coil is cut in two equal halves and the two pieces are joined in parallel to the same source. The energy now liberated per second is
View SolutionA heating coil transforms 100J of electrical energy into heat energy per second. The coil is cut into two halves and both the halves are joined togeter in parallel to the same source. Now the energy transformed per second will be
View Solutionn identical condenser are joined in parallel and are charged to potential V. Now they are separated and joined in series. Then the total energy and potential difference of the combination will be
View Solution
