In a potentiometer experiment , the balancing length for a cell was found to the 1.20 m . Now , a resistance of 10Ω is connected across the terminals of this cell and the balancing length becomes 80 cm . The internal resistance of this cell is .
2Ω
5Ω
1.5Ω
15Ω
The correct Answer is:B
To solve the problem of finding the internal resistance of the cell in a potentiometer experiment, we can follow these steps:
Step 1: Understand the Setup
In a potentiometer experiment, we have two scenarios:
1. When the switch is open, the balancing length L1 is measured.
2. When a resistance R is connected across the cell and the switch is closed, the new balancing length L2 is measured.
Step 2: Write Down the Given Values
From the problem statement, we have:
- L1=1.20m (or 120 cm)
- L2=0.80m (or 80 cm)
- R=10Ω (the resistance connected across the terminals of the cell)
Step 3: Apply the Potentiometer Principle
According to the potentiometer principle, the voltage drop across the lengths of the wire is proportional to the lengths measured. Therefore, we can write the following equations based on the two scenarios:
1. When the switch is open:
E=k⋅L1
2. When the switch is closed:
E=(R+r)⋅Iwhere I=ER+r
The voltage drop across the potentiometer wire is:
V′=k⋅L2
Step 4: Set Up the Ratio of the Two Scenarios
Since both scenarios measure the same electromotive force E, we can equate them:
k⋅L1=(R+r)⋅I
And for the second scenario:
k⋅L2=R⋅I
Step 5: Form the Equations
From the first scenario:
E=k⋅L1
From the second scenario:
E=k⋅L2+R⋅I
Step 6: Take the Ratio of the Two Equations
Taking the ratio of the two equations gives:
L1L2=R+rR
Step 7: Substitute Known Values
Substituting the known values into the ratio:
120cm80cm=10+r10
This simplifies to:
32=10+r10
Step 8: Cross Multiply and Solve for r
Cross multiplying gives:
3⋅10=2⋅(10+r)
30=20+2r
30−20=2r
10=2r
r=5Ω
Final Answer
The internal resistance of the cell is r=5Ω.
---
In a potentiometer experiment, we have two scenarios:
1. When the switch is open, the balancing length L1 is measured.
2. When a resistance R is connected across the cell and the switch is closed, the new balancing length L2 is measured.
From the problem statement, we have:
- L1=1.20m (or 120 cm)
- L2=0.80m (or 80 cm)
- R=10Ω (the resistance connected across the terminals of the cell)
According to the potentiometer principle, the voltage drop across the lengths of the wire is proportional to the lengths measured. Therefore, we can write the following equations based on the two scenarios:
E=k⋅L1
2. When the switch is closed:
E=(R+r)⋅Iwhere I=ER+r
The voltage drop across the potentiometer wire is:
V′=k⋅L2
Since both scenarios measure the same electromotive force E, we can equate them:
k⋅L1=(R+r)⋅I
And for the second scenario:
k⋅L2=R⋅I
From the first scenario:
E=k⋅L1
From the second scenario:
E=k⋅L2+R⋅I
Taking the ratio of the two equations gives:
L1L2=R+rR
Substituting the known values into the ratio:
120cm80cm=10+r10
This simplifies to:
32=10+r10
Cross multiplying gives:
3⋅10=2⋅(10+r)
30=20+2r
30−20=2r
10=2r
r=5Ω
The internal resistance of the cell is r=5Ω.
Similar Questions
In a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
View SolutionIn potentiometer experiment when terminates of the cell is at distance of 52 cm, then no current flows through it. When 5ohm shunt resistance is connected in it then balance length is at 40 cm. The internal resistance of the cell is
View Solution
Knowledge Check
In a potentiometer experiment , the balancing length for a cell was found to the 1.20 M . Now , a resistance of 10Ω is connected across the terminals of this cell and the balancing length becomes 80 cm . The internal resistance of this cell is .
A2ΩB5ΩC1.5ΩD15ΩThe emf of cell is balanced by balancing length 450 cm . When the resistance of 10Ω is connected across the cell, balancing length changes by 100 cm. The internal resistance of a cell is
A1.8ΩB2.8ΩC3.8ΩD2.5ΩIn a potentiometer experiment, the balancing length with a cell is 560cm. When an external resistance of 10ohms is connected in parallel to the cell the balancing length changs by 60cm. The internal resistance of the cell in ohm is
A3.6B2.4C1.2D0.6
Null point in the galvanometer is obtained when a cell of emf E and internal resisance r is connncted across the length of 22 cm wire of the potentiometer . Now a resistane of 10Ω is connected across the terminals of the cell (by closing the key K) and null point is obtained against the length of cm. The internal resistance r of the cell is -
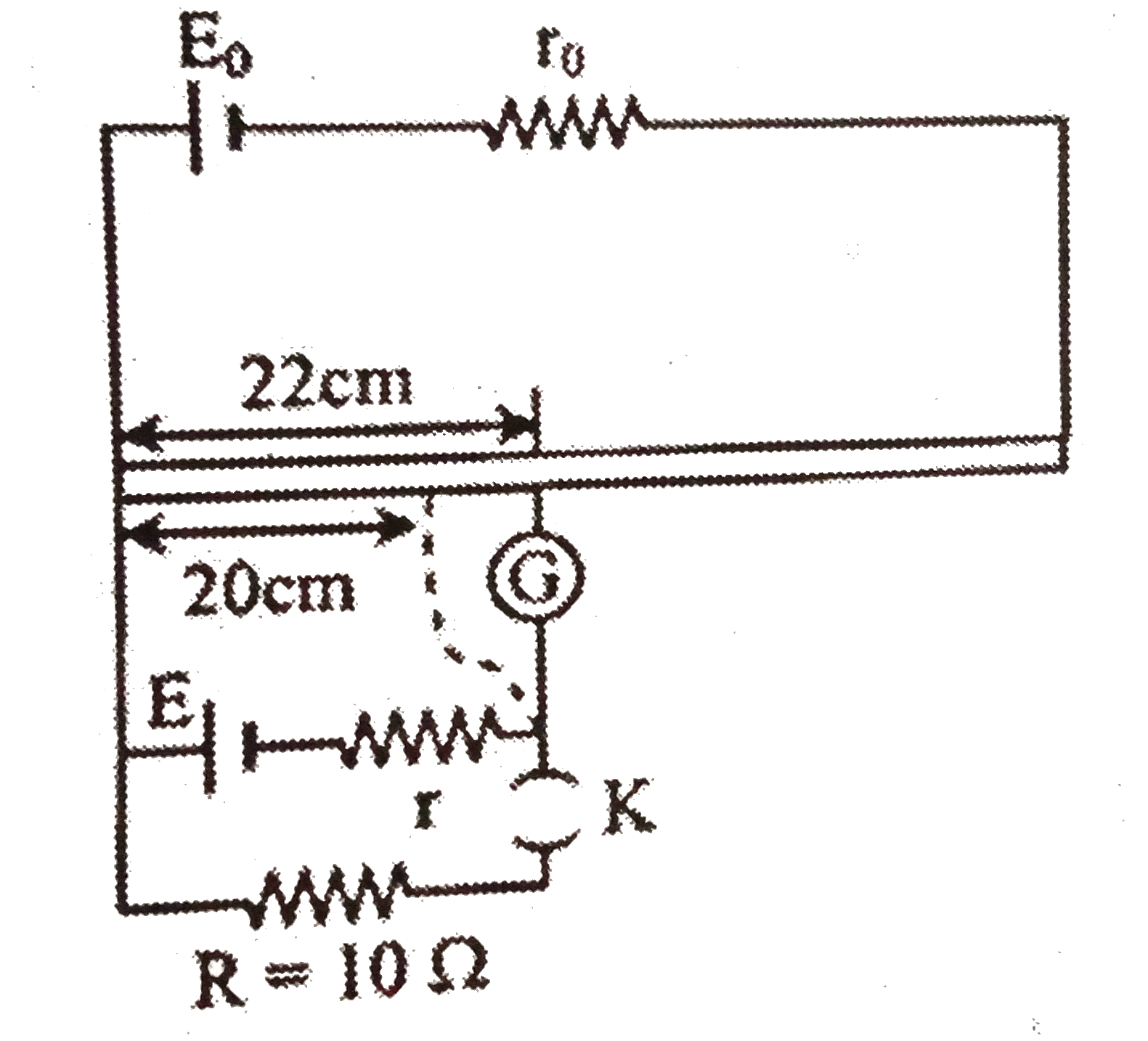
View SolutionIn a potentiometer experiment the balancing with a cell is at length 240 cm. On shunting the cell with a resistance of 2Ω, the balancing length becomes 120 cm.The internal resistance of the cell is
View SolutionIn a potentiometer experiment the balancing with a cell is at length 240 cm. On shunting the cell with a resistance of 2Ω, the balancing length becomes 120 cm.The internal resistance of the cell is
View SolutionA 2.0 V potentiometer is used to determine the internal resistance of 1.5V cell. The balance point of the cell in the circuit is 75cm. When a resistor of 10Ω is connected across cel, the balance point sifts to 60cm. The internal resistance of the cell is
View SolutionIn a potentiometer experiment, the balancing length is found to be 1.8 m for a cell of e.m.f. 1.5 V. What is the balancing length for a cell of e.m.f. 1 V ?
View Solution
