A : A low voltage supply from which high currents are to be withdraw , must have very low internal resistance .
R : Maximum current drawn from a source is inversely proprtional to internal reisistance .
If both Assertion & Reason are true and the reason is the correct explanation of the assertion , then mark
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion then mark.
If Assertion is ture statement but Reason is false , then mark
If both Assertion and Reason are false statements then mark.
The correct Answer is:A
To solve the given problem, we need to analyze the assertion (A) and the reason (R) provided in the question.
1. Understanding Assertion (A):
- The assertion states that a low voltage supply from which high currents are to be withdrawn must have very low internal resistance.
- According to Ohm's Law, the current (I) flowing through a circuit is given by the formula:
I=VR
where V is the voltage and R is the resistance.
2. Analyzing the Condition:
- In this case, since the voltage V is low, to achieve a high current I, the resistance R must be low.
- Therefore, if we want to draw high currents from a low voltage supply, we indeed require a very low internal resistance.
3. Understanding Reason (R):
- The reason states that the maximum current drawn from a source is inversely proportional to the internal resistance.
- This can be expressed mathematically as:
I∝1R
- This means that as the internal resistance R decreases, the current I increases, which supports the assertion.
4. Conclusion:
- Both the assertion (A) and the reason (R) are correct.
- Furthermore, the reason correctly explains the assertion. Therefore, the answer to the question is that both A and R are true, and R provides a correct explanation for A.
Final Answer:
Both Assertion (A) and Reason (R) are correct, and R explains A.
---
- The assertion states that a low voltage supply from which high currents are to be withdrawn must have very low internal resistance.
- According to Ohm's Law, the current (I) flowing through a circuit is given by the formula:
I=VR
where V is the voltage and R is the resistance.
- In this case, since the voltage V is low, to achieve a high current I, the resistance R must be low.
- Therefore, if we want to draw high currents from a low voltage supply, we indeed require a very low internal resistance.
- The reason states that the maximum current drawn from a source is inversely proportional to the internal resistance.
- This can be expressed mathematically as:
I∝1R
- This means that as the internal resistance R decreases, the current I increases, which supports the assertion.
- Both the assertion (A) and the reason (R) are correct.
- Furthermore, the reason correctly explains the assertion. Therefore, the answer to the question is that both A and R are true, and R provides a correct explanation for A.
Both Assertion (A) and Reason (R) are correct, and R explains A.
Similar Questions
Knowledge Check
A dry cell has an e.m.f. of 1.5V and an internal resistance of 0.05Ω. The maximum current obtainable from this cell for a very short time interval is
A30AB300AC3AD0.3AA : High voltage ( high tension ) supply must have very large internal resistance.
R: If the circuit is accidentally shorted , then the current drawn will not exceed safely limits if internal resistance is high.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion , then markBIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion then mark.CIf Assertion is ture statement but Reason is false , then markDIf both Assertion and Reason are false statements then mark.In a circuit a cell with internal resistance r is connected to an external resistance R. The condition for the maximum current that drawn from the cell is
AR=rBR<rCR>rDR=0
Answer the following questions : (a) A steady current flows in a metallic conductor of non-uniform cross-section. Explain which of these quantities is constant along the conductor : current, current density, electric field and drift speed ?
(b) Is Ohm's law universally applicable for all conducting elements ? If not, give examples of elements which do not obey Ohm's law.
(c) A low voltage supply from which one needs high currents must have low internal resistance, why ?
(d) A high tension (HT) supply of say 6kV must have a very large internal resistance. why ?
View SolutionA cell of internal resistance r connected across an external resistance R can supply maximum current when
View SolutionAn total resistance R is connected to a cell of internal resistance r the maximum current flows in the external resistance, when
View Solution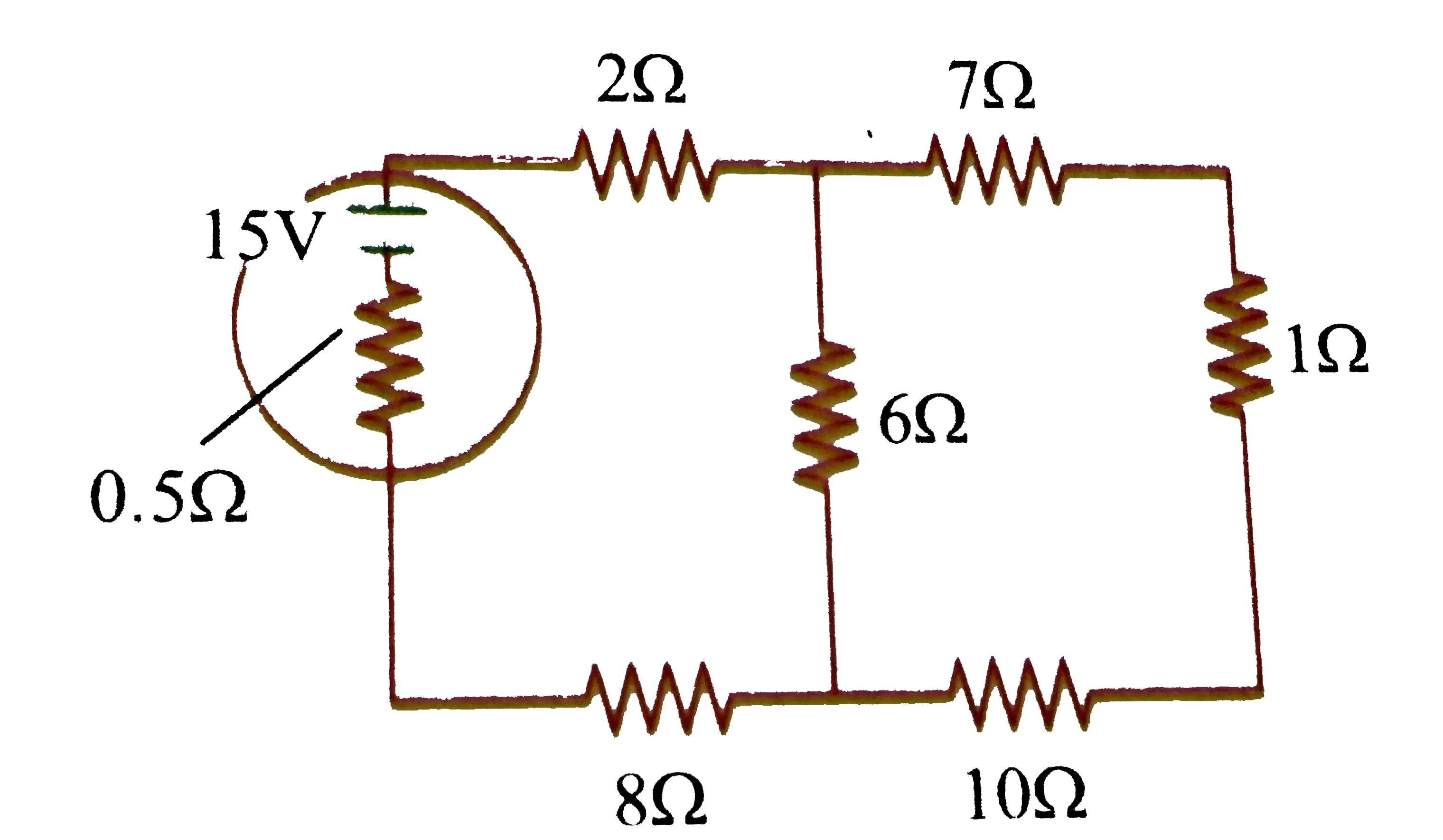
The emf of a cell E is 15 V as shown in the figure with an internal resistance of 0.5Ω. Then the value of the current drawn from the cell is
View SolutionThe maximum current can be drawn from which of the following cells?
View Solution
