Rod particle collisions and Angular Impulse
Step by step video solution for Rod particle collisions and Angular Impulse by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the angular momentum of the particle and of then about the centre of mass C before the collision.AM2mvl4(M+m)2,m2Mvl4(m+M)BM2mvl2(M+m)2,M2Mvl2(m+M)CM2mvl(M+m)2,m2Mvl(m+M)D2M2mvl(M+m)2,2m2Mvl(m+M)A Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
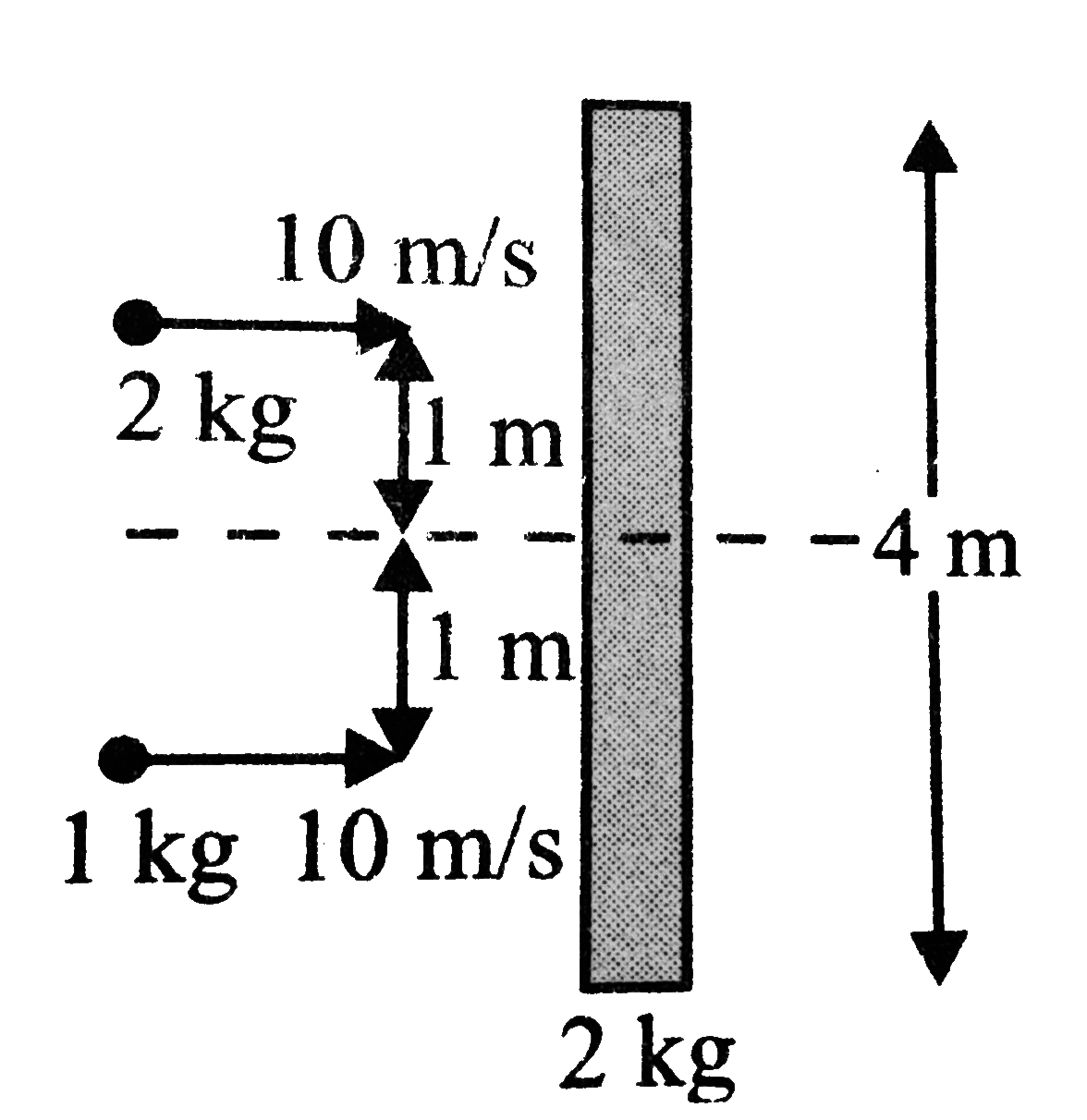
Angular velocity of the rod after collision isA1117rad/sBrad/sC1917rad/sD3017rad/sA rod of mass m and length l in placed on a smooth table. An another particle of same mass m strikes the rod with velocity v0 in a direction perpendicular to the rod at distance x(<l/2) from its centre . Particle sticks to the end. Let ω be the angular speed of system after collision , then
Find the maximum possible value of impulse (by varying x) that can be imparted to the particle during collision. Particle still sticks to the rod.Amv02B2mv03C3mv04D4mv05
What is angular impulse ?
View SolutionA particle of mass m is moving perpendicular to a rod of length L kept on a frictionless horizontal surface and collides at a distance L/4 from the centre of rod. Particle comes to state of rest just after collision. Mass of rod is M and speed of particle before collision is u. Let v is the velocity of centre of rod after collision and is angular velocity attained by the rod. Find Lωv
View SolutionQuestions on Angular Momentum and Angular Impulse
View SolutionImportant Questions|Angular Impulse|OMR
View SolutionTwo particles each of mass M are connected by a massless rod. The rod is lying on the smooth horizontal surface. If one of the particle is given an impulse MV as shown in the figure then angular velocity of the system would be:
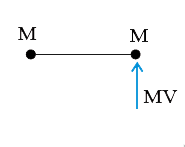
View Solution
