एक आदर्श सरल लोलक की कुल ऊर्जा संरक्षित रहती है सरल लोलक की भिन्न अवस्थाओं में ऊर्जा की गणना कर इस कथन की सिद्ध कीजिये।

Video Solution

Text Solution

Verified by Experts

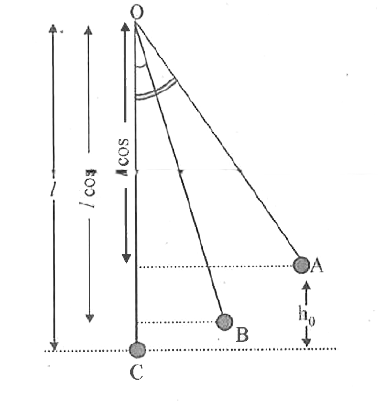
मान ले की द्रव्यमान m एवं लम्बाई l का एक आदर्श सरल लोलक अपनी उर्ध्व स्थिति से अधिकतम $θ_{0}$ कोण बनाते हुए माध्य स्थिति (OB) के इर्द गिर्द दोलन कर रहा है। किसी मध्यवर्ती स्थिति पर यह माध्य स्थिति (OC) के साथ $θ$ कोण बना रहा है ।
निर्देश स्तर निम्नतम बिंदु C पर तथा उच्चतम स्तर बिंदु A पर है , जैसा की चित्र दर्शाया गया है ।
यहाँ $h_{0} = l - l {cos θ}_{0}$
या $h_{0} = l (l - {cos θ}_{0})$
तथा $h = l (1 - cos θ)$
सरल लोलक बिंदु A की स्थिति से छोड़ा जाता है , जहां उसका प्रारंभिक वेग u = 0 होता है।
$∴$ चरम स्थिति बिंदु A पर -
गतिज ऊर्जा
$E_{K_{A}} = \frac{1}{2} {mu}^{2} = \frac{1}{2} m {(0)}^{2} = 0$
स्थितिज ऊर्जा
$E_{P_{A}} = m g (1 - {cos θ}_{0})$
अतः कुल यांत्रिक ऊर्जा
$E_{A} = E_{K_{A}} + E_{P_{A}}$
या $E_{A} = E_{K_{A}} + E_{P_{A}}$
या $E_{A} = 0 + m g l (1 - {cos θ}_{0})$
या $E_{A} = m g l (1 - cos θ)$ (1)

किसी मध्यवर्ती स्थिति के बिंदु B पर -
बिंदु पर पहुंचते - पहुंचते लोलक द्वारा अर्जित वेग हो जाता है तथा निर्देश स्तर से ऊँचाई हो जाती है। तब गति के तृतीय समीकरण से ,
$V_{B}^{2} = u^{2} + 2 g (h_{0} - h)$
या $V_{B}^{2} = 2 g l (cos θ - {cos θ}_{0}) = l (1 - cos θ)]$ या
$V_{B}^{2} = 2 g l (cos θ - {cos θ}_{0})$
$∴$ गतिज ऊर्जा
$E_{K_{B}} = \frac{1}{2} m \times 2 g l (cos θ - {cos θ}_{0})$
या $E_{K_{B}} = m g l (cos θ = {cos θ}_{0})$
तथा स्थितिज ऊर्जा
$E_{B} = E_{K_{B}} + E_{P_{B}}$
या $E_{B} = m g l (cos θ - {cos θ}_{0}) + m g l (1 - cos θ)$
$∴ E_{B} = m g l (1 - {cos θ}_{0}) ... (2)$
माध्य स्थिति के निर्देश स्तर निम्नतम बिंदु C पर
लोलक C जब बिन्दु पर पहुँचता है , तब उसका वेग $v_{B}$ हो जाता है तथा निर्देश स्तर से ऊँचाई शून्य हो जाती है ।
$∴$ गति के तृतीय समीकरण से ,
$v_{c}^{2} = u^{2} + 2 g h_{0}$
$v_{c}^{2} = {(0)}^{2} + 2 g l (1 - {cos θ}_{0})$
अतः गतिज ऊर्जा
$E_{K_{C}} = \frac{1}{2} m v_{c}^{2}$
या $E_{K_{C}} = \frac{1}{2} m \times 2 g l (1 - {cos θ}_{0})$
तथा स्थितिज ऊर्जा $E_{P_{C}} = (m g) (0)$
$∴ E_{P_{C}} = 0$
$∴$ कुल यांत्रिक ऊर्जा $E_{C} = E_{K_{C}} + E_{P_{C}}$
या $E_{C} = m g l (1 - {cos θ}_{0}) + 0$
या $E_{C} = m g l (1 - {cos θ}_{0})$ ...(3)
समीकरण (1) ,(2),(3) की तुलना से ,
$E_{A} = E_{B} = E_{C} = m g l (1 - {cos θ}_{0})$ = नियतांक ..(4)
अतः एक आदर्श सरल लोलक की कुल यांत्रिक ऊर्जा के प्रत्येक स्थिति में संरक्षित बनी रहती है , जब माध्य स्थिति के इर्द गिर्द दोलन करता है ।

|

Updated on:21/07/2023

Class 10 PHYSICS कार्य, ऊर्जा और शक्ति

Topper's Solved these Questions

Similar Questions

SANJEEV PUBLICATION-कार्य, ऊर्जा और शक्ति -अन्य महत्त्वपूर्ण प्रश्न (निबंधात्मक प्रश्न)

Home
Ask Doubt
Profile