For sets A,B, and C using Venn diagram , check if A-(B-C) = (A-B-C)
To determine if A−(B−C)=(A−B)−C using Venn diagrams, we can follow these steps:
Step 1: Understand the Sets
We have three sets: A, B, and C. We need to analyze the expressions A−(B−C) and (A−B)−C.
Step 2: Find B−C
The expression B−C represents the elements that are in set B but not in set C. In a Venn diagram, this is the area of set B that does not overlap with set C.
Step 3: Find A−(B−C)
Now, we need to subtract B−C from A. This means we will shade the area of A that does not include the area of B that is not in C. The remaining shaded area will represent A−(B−C).
Step 4: Find A−B
Next, we need to find A−B. This represents the elements that are in A but not in B. In the Venn diagram, this is the area of A that does not overlap with set B.
Step 5: Find (A−B)−C
Now, we need to subtract C from A−B. This means we will shade the area of A−B that does not include the area of C. The remaining shaded area will represent (A−B)−C.
Step 6: Compare the Two Areas
Finally, we compare the shaded areas from steps 3 and 5. If the shaded areas are the same, then A−(B−C)=(A−B)−C. If they are different, then the two expressions are not equal.
Conclusion
After analyzing the Venn diagram, we can conclude that the two expressions are not equal, hence A−(B−C)≠(A−B)−C.
We have three sets: A, B, and C. We need to analyze the expressions A−(B−C) and (A−B)−C.
The expression B−C represents the elements that are in set B but not in set C. In a Venn diagram, this is the area of set B that does not overlap with set C.
Now, we need to subtract B−C from A. This means we will shade the area of A that does not include the area of B that is not in C. The remaining shaded area will represent A−(B−C).
Next, we need to find A−B. This represents the elements that are in A but not in B. In the Venn diagram, this is the area of A that does not overlap with set B.
Now, we need to subtract C from A−B. This means we will shade the area of A−B that does not include the area of C. The remaining shaded area will represent (A−B)−C.
Finally, we compare the shaded areas from steps 3 and 5. If the shaded areas are the same, then A−(B−C)=(A−B)−C. If they are different, then the two expressions are not equal.
After analyzing the Venn diagram, we can conclude that the two expressions are not equal, hence A−(B−C)≠(A−B)−C.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Exercise 1.112videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGECHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Exercise 1.28videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGECHAPTER - SEQUENCE AND SERIESEXERCISE - Question Bank36videos
SEQUENCE AND SERIES
- BOOK - CENGAGECHAPTER - SETS AND RELATIONSEXERCISE - Question Bank15videos
SETS AND RELATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If A, B and C are three sets, then A-(B-C) equals to
AA) A−(B∩C)BB) (A−B)∪CCC) (A−B)∪(A∩C)DD) (A−B)∪(A−C) - Question 2 - Select One
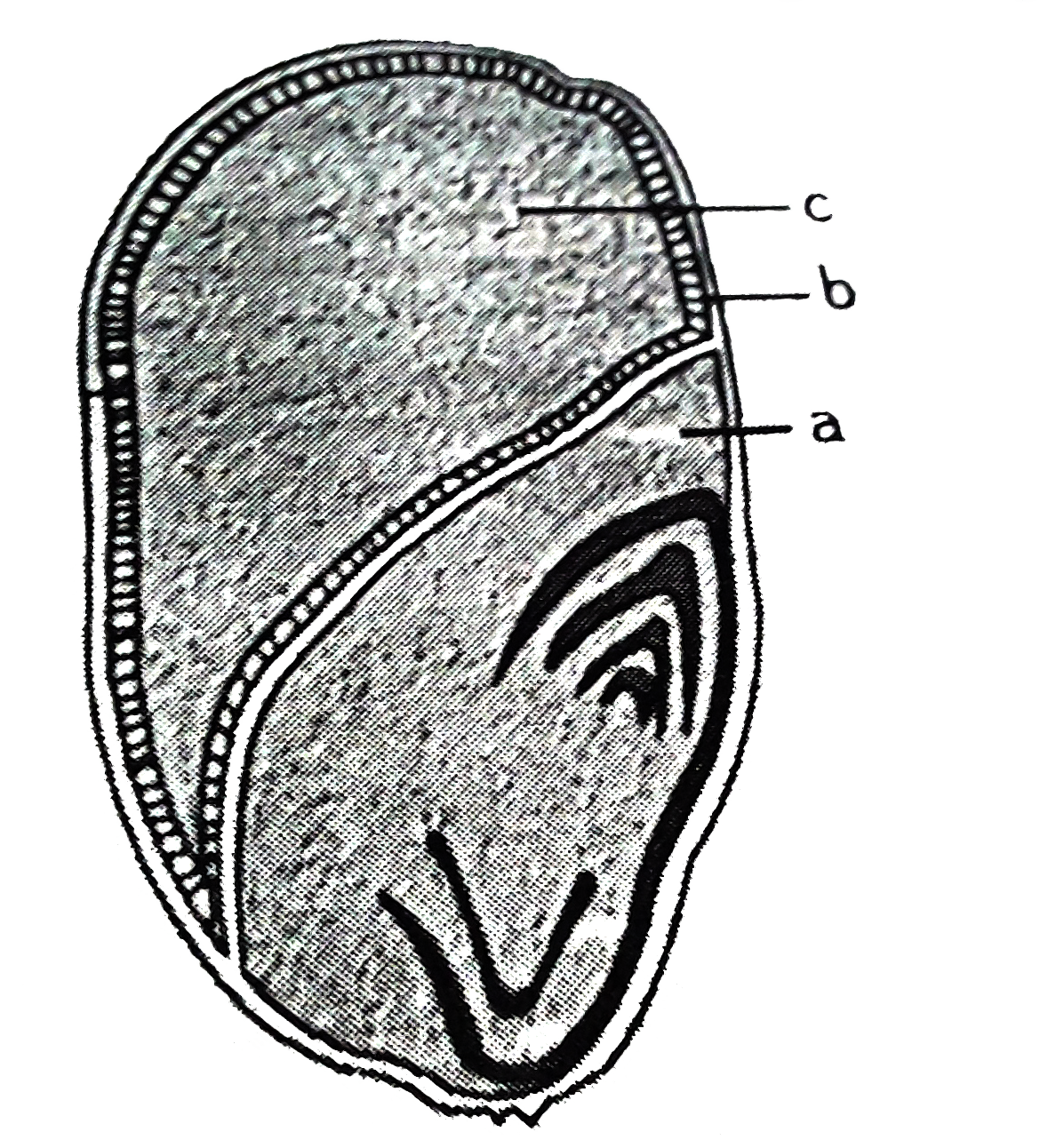
In the diagram identify A, B and C.
 AA - Reissner's membrane , B - Organ of corti , C - Basilar membraneBA - Reissner's membrane , B - Tectorial membrane , C - Basilar membraneCA - Scala vestibuli , B - Scala media , C - Scala tympaniDA - Tectorial membrane , B - Reissner's membrane , C - Basilar membrane
AA - Reissner's membrane , B - Organ of corti , C - Basilar membraneBA - Reissner's membrane , B - Tectorial membrane , C - Basilar membraneCA - Scala vestibuli , B - Scala media , C - Scala tympaniDA - Tectorial membrane , B - Reissner's membrane , C - Basilar membrane
Let A={2,4,6,8,10},B={4,8,12,16}andC={6,12,18,24}.
Using Venn diagrams, verify that:
(i) (A∪B)∪C=A∪(B∪C)
(ii) (A∩B)∩C=A∩(B∩C)View SolutionDraw venn diagram of (A∩C) .
View Solution2. LetA 12, 4, 6, 8, 10), B f4, 8, 12, 16) and C 16, 12, 18, 24) Using Venn diagrams, verify that (i) (A u B) u C Au (B u C)
View SolutionFor all sets A, B and C,A−(B−C)=(A−B)−C.
View SolutionLet A=(a,e,i,o,u},B={a,d,e,o,v}andC{e,o,t,m}.
Using Venn diagrams, verify the following :
(i) A∪(B∩C)=(A∪B)∩(A∪C)
(ii) A∩(B∪C)=(A∩B)∪(A∩C).View SolutionFor any three sets A, B and C, prove that:
(A−B)×C=(A×C)−(B×C)View Solution