The complete solution set of inequality $\frac{{(x - 5)}^{1005} {(x + 8)}^{1008} (x - 1)}{x^{1006} {(x - 2)}^{3} {(x - 3)}^{5} (x - 6) {(x + 9)}^{1010}} \leq 0$

A

$(- \infty, - 9) \cup (- 8, 0) \cup (0, 1) \cup (2, 3) \cup [5, 6]$

B

$(- \infty, - 9) \cup (- 9, 0) \cup (0, 1) \cup (2, 3) \cup [5, 6)$

C

$(- \infty, - 9) \cup (- 9, 0) \cup (0, 1] \cup (2, 3) \cup [5, 6)$

D

$(- \infty, 0) \cup (0, 1] \cup (2, 3) \cup [5, 6)]$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

We have $\frac{{(x - 5)}^{1005} {(x + 8)}^{1008} (x - 1)}{x^{1006} {(x - 2)}^{3} {(x - 3)}^{5} (x - 6) {(x + 9)}^{1010}} \leq 0$

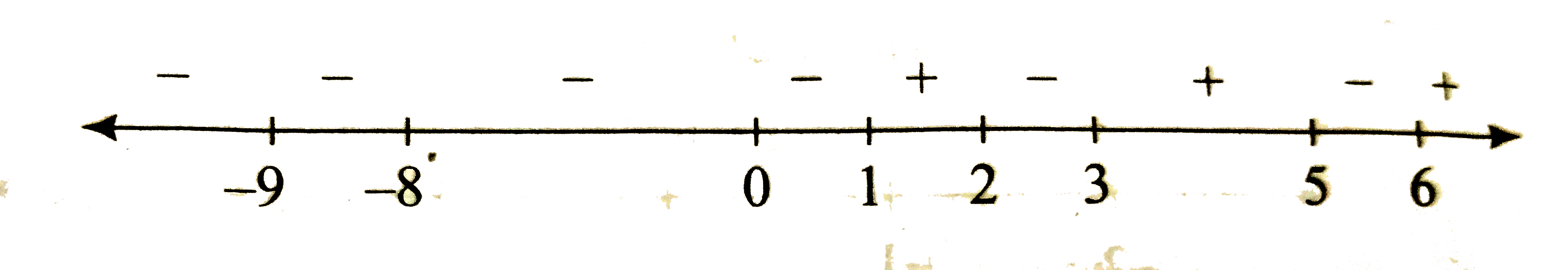
From the sign scheme $x \in (- \infty, 9) \cup (- 9, 0) \cup (0, 1) \cup (2, 3) \cup [5, 6)$

|

Updated on:21/07/2023

Class 12 MATHS SET THEORY AND REAL NUMBER SYSTEM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Solution set for inequality $| x - 1 | \leq 5$ is.
A[-6,4]
B[-4,0]
C[-4,6]
D[0,6]
Question 2 - Select One
Complete solution set of inequlaity $\frac{(x + 2) (x + 3)}{(x - 2) (x - 3)} \leq 1$
A $(- \infty, 0)$
B $(- \infty, 0] \cup (2, 3)$
C[2,3]
D $(- \infty, 2) \cup (3, \infty)$
Question 3 - Select One
Complete solution set of the inequality $∣ ∣ x^{2} - x - 2 ∣ ∣ + | x + 1 | \leq 0$ is
A $(- \infty, - 1)$
B $(- 1, 0)$
C ${- 1, 0}$
D ${- 1}$

CENGAGE-SET THEORY AND REAL NUMBER SYSTEM -Exercises

Home
Ask Doubt
Profile