Question

A vertical tower PQ subtends the same anlgle of ${\displaystyle {30}^{\circ }}$ at each of two points A and B ,60 m apart on the ground .If AB subtends an angle of ${\displaystyle {120}^{\circ }}$ at p the foot of the tower ,then find the height of the tower .

Explanation

In triagle APQ, we have

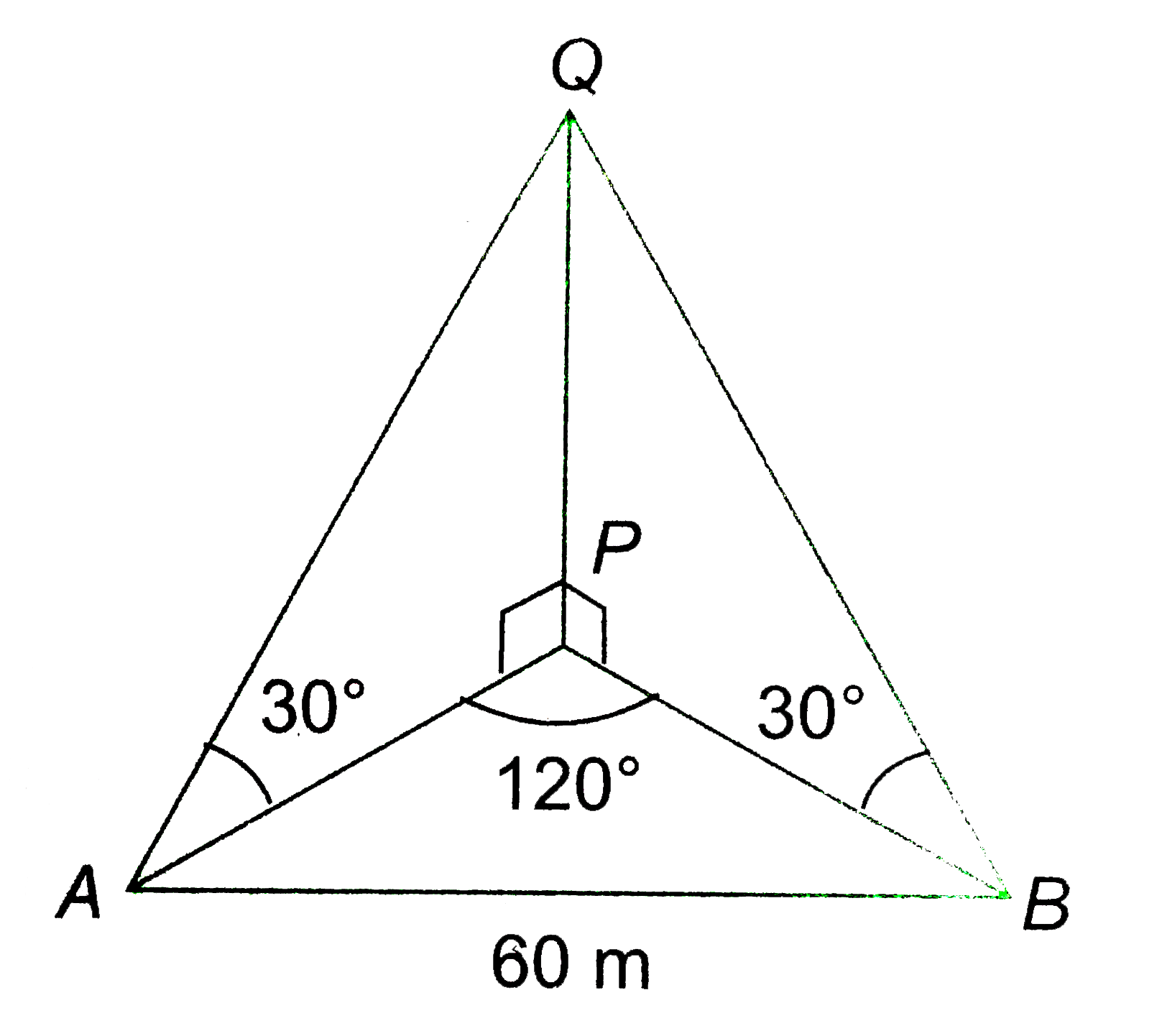
AP = PQ cot `30^@=sqrt(3)PQ`
In triangle BPQ we have
BP= PQ cot `30^@=sqrt(3)PQ`
In `Delta`APB using cosine rule ,we get
` cos 120^@ =(AP^2+BP^2-AB^2)/(2 AP.BP)`
`rArr - 1/2 = (6 PQ^2 - 60 ^2)/(2.3 PQ^2)`
`rArr 9 PQ^2= 60 ^2`
` PQ= 20 m `