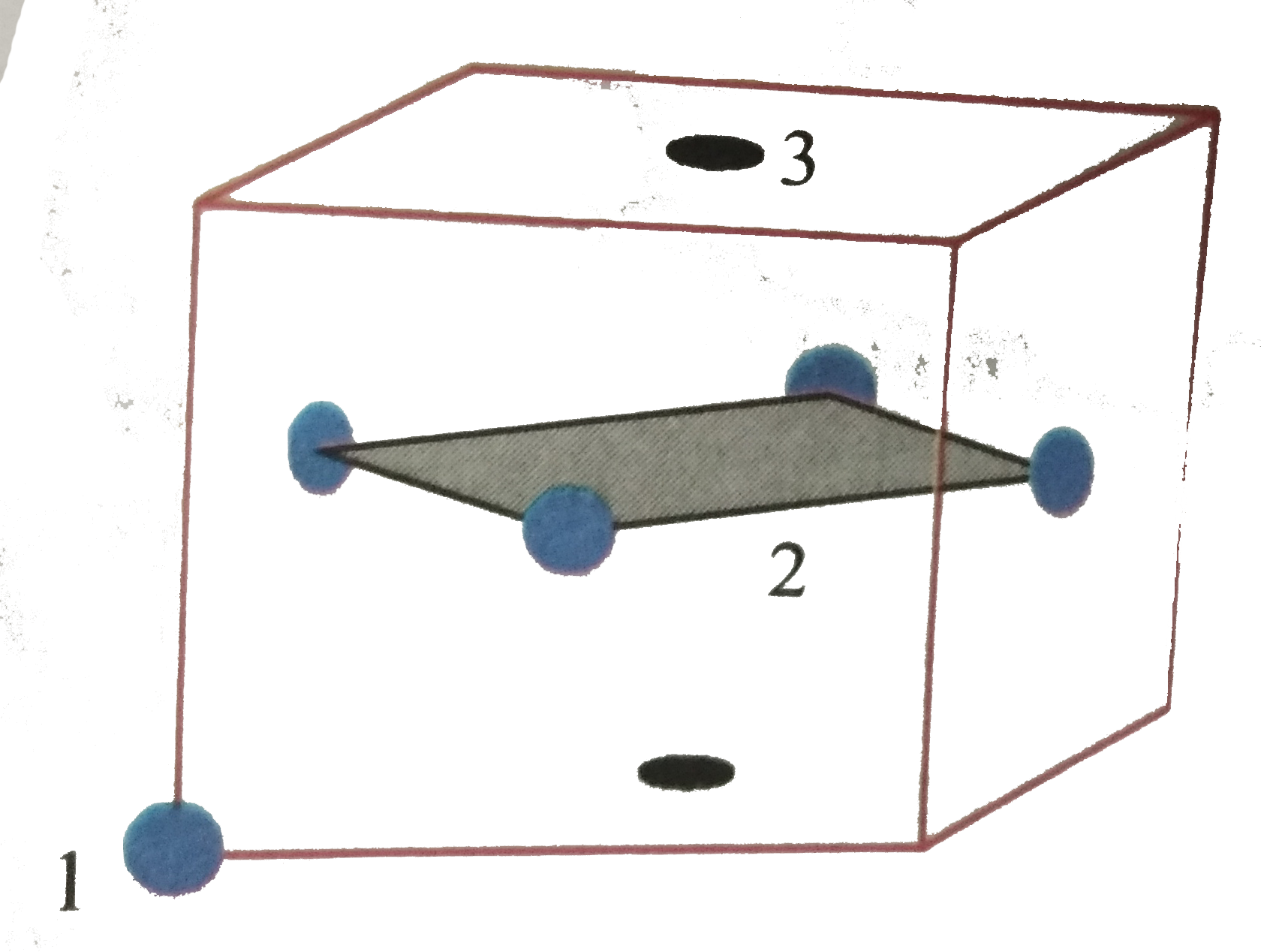
Following figure shows an FCC unit cell with atoms of radius r market 1(corner), 2(face centre), 3(face centre). A quadrilateral is also shown by joining the centers of 4 face centered atoms.
Find : (i) The distances between atoms 1& 2, 2 &3, and 1 &3
(ii) The shape and dimensions of the quadrilateral

The correct Answer is:(i) 2r, 2r, 2√3r; (ii) square, side = 2r
Topper's Solved these Questions
- SOLID STATEBook:RESONANCEChapter:SOLID STATEExercise:Part-II : Only one option correct type
Explore 42 Videos
- SOLID STATEBook:RESONANCEChapter:SOLID STATEExercise:Part-III : Match the column
Explore 3 Videos
- SOLID STATEBook:RESONANCEChapter:SOLID STATEExercise:Miscellaneous solved problems
Explore 16 Videos
- S BLOCK ELEMENTSBook:RESONANCEChapter:S BLOCK ELEMENTSExercise:INORGANIC CHEMISTRY(s-Block Elements)
Explore 36 Videos
- STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYBook:RESONANCEChapter:STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYExercise:Section -B
Explore 18 Videos
Similar Questions
Following figure shows an FCC unit cell with atoms of radius r marked 1 (corner),2 (face center),3 (face center). A quadrillateral is also shown by joining the centers of 4 face centered atoms. The distances between atoms 1 & 2,2, & 3 and 1&3.
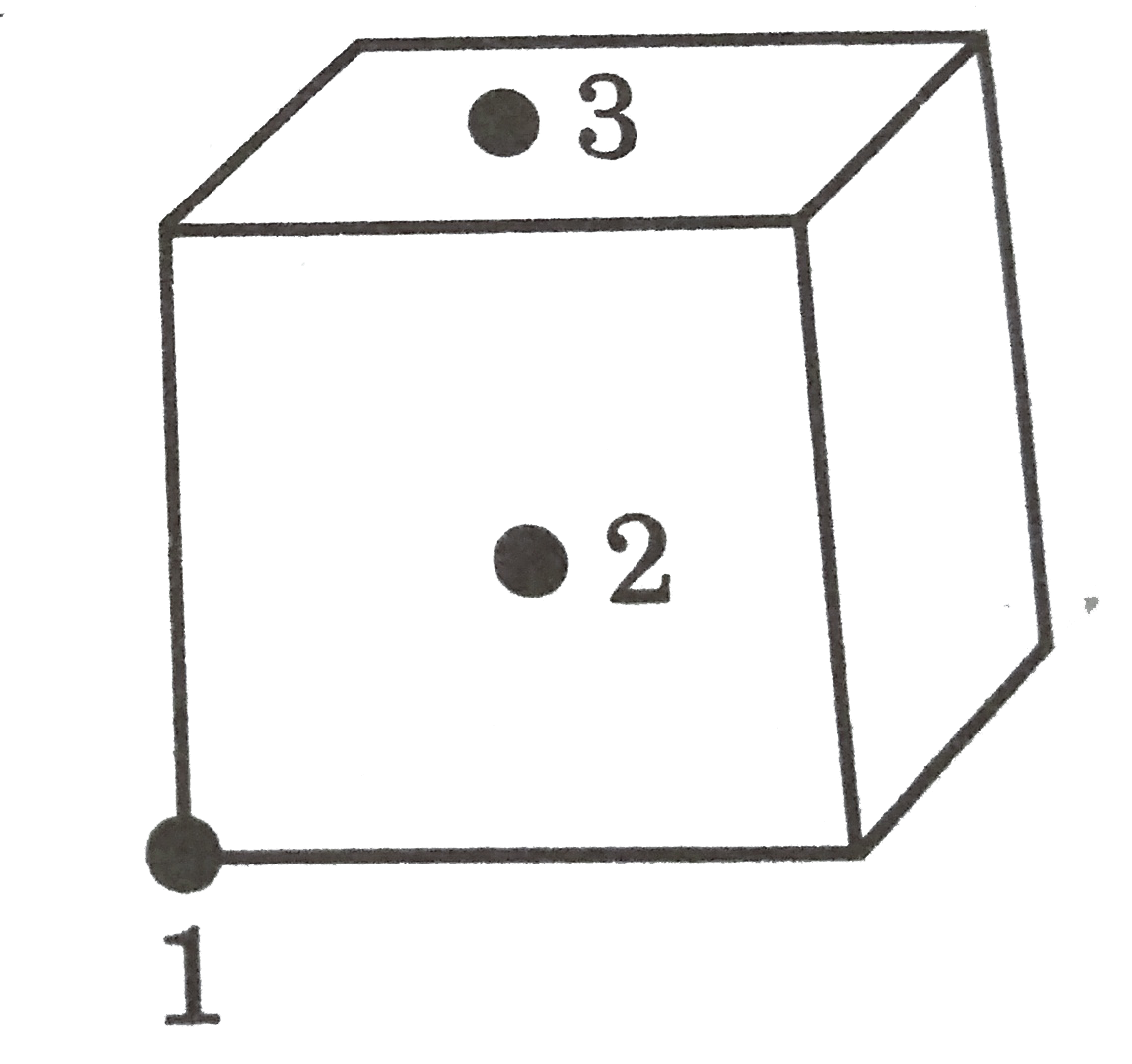
View SolutionFigure shows a cube of unit cell of CCP arrangements with face centred atoms marked 1,2, 3. Which of the following is true?
View Solution
Knowledge Check
Total volume of atoms present in a face centred cubic unit cell of a metal is (r=radius of atom)
A203πr3B243πr3C123πr3D163πr3In a solid AB having NaCl structure 'A' atoms occupy the corners & face centre of the cubic unit cell. If all the face centered atoms along one of the axes are removed, then the resultant stoichiomery of the solid is
AAB2BA2BCA4B3DA3B4Total volume of atoms present in a face centred cubic unit cell of a metal is (r=atomic radius)
A203πr3B243πr3C123πr3D163πr3
Atoms A, B, C and D are present at corners, face centres, body centres and edge centres and respectively in a cubic unit cell. Find the formula of compound.
View SolutionAtoms A, B, C and D are present at corners, face centres, body centres and edge centres and respectively in a cubic unit cell. Find the formula of compound.
View SolutionAtoms A, B, C and D are present at corners, face centres, body centres and edge centres and respectively in a cubic unit cell. Find the formula of compound.
View SolutionAtoms A, B, C and D are present at corners, face centres, body centres and edge centres and respectively in a cubic unit cell. Find the formula of compound.
View SolutionIf r is the radius of an atom in face-centred cubic unit cell of edge length a then
View Solution
