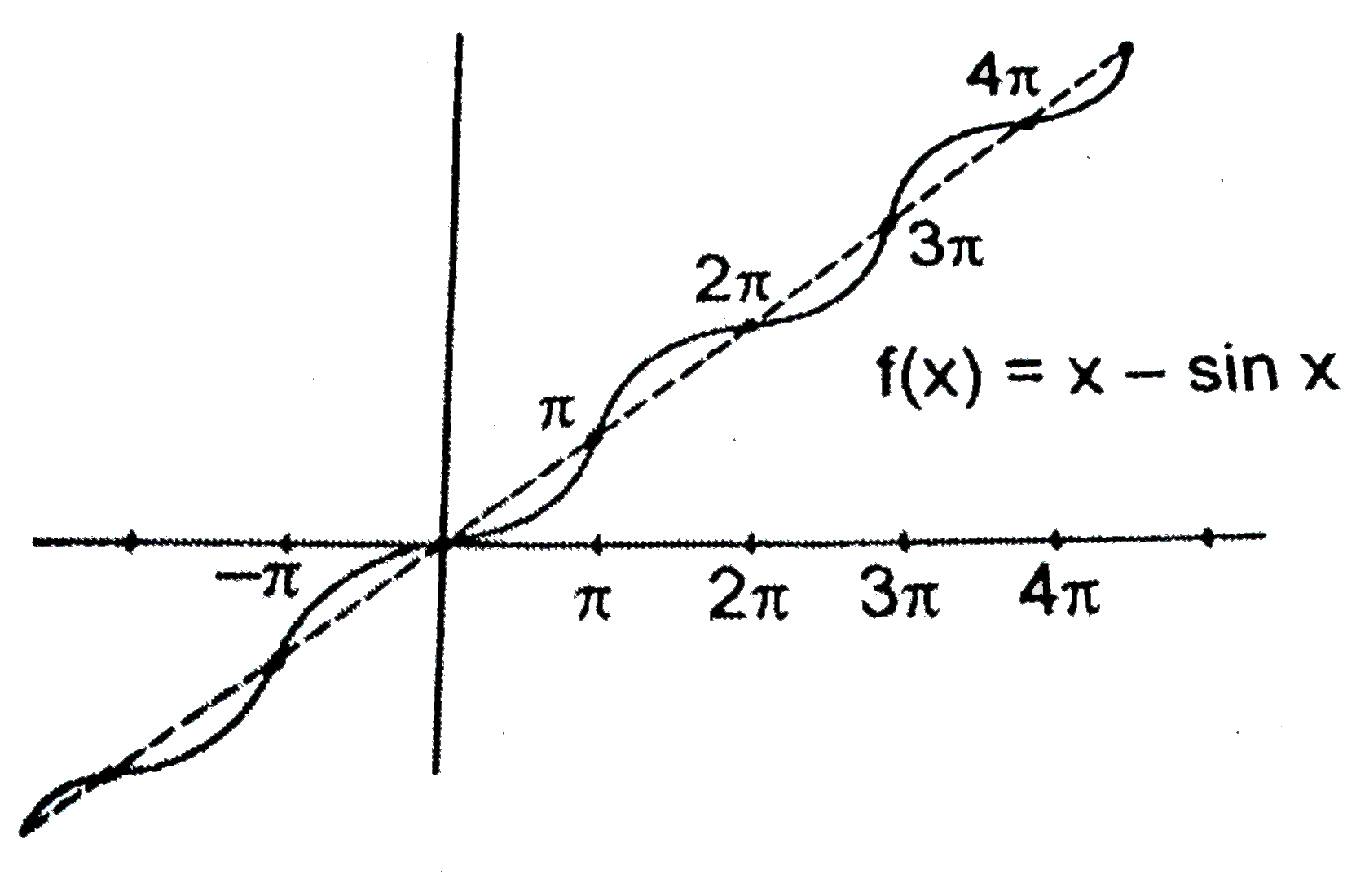
Let f(x)=x- sinx. Find the intervals of monotonicity.
f'(x)=1−cosx
Now f'(x) >0 every where except at x=0,±2π±4π etc. But all these points are discrete (countble) and do not form an interval. Hence we can conclude that f(x) is stricitly increasing in R. In fact we can also see it graphically.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Self Practice Problems34videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1A5videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)8videos
COMBINATORICS
Similar Questions
f(x)=x−sinx. Find the intervals of monotonicity.
View SolutionLet f (x)=x3. Find the intervals of monotonicity.
View SolutionThe graph of the derivative f' of a continuous function f is shown with f(0)=0, then for f(x) find (i) Intervals of monotonicity (ii) Intervals of concavity
View SolutionFind the interval of monotonicity of y=1−x+x21+x+x2
View SolutionFind the intervals of monotonicity of the following f(x)=2x2−ln|x|
View SolutionDetermine the intervals of monotonicity for the following functions :
f(x)=ln|x|,View SolutionDetermine the intervals of monotonicity for the following functions :
f(x)=2x3−9x2−24x+7,View SolutionDetermine the intervals of monotonicity for the following functions :
f(x)=4x3−21x2+18x+20,View SolutionLet f(x)=ex+sinx be defined on the interval [–4, 0]. Find the odd and even extension of f(x) in the interval [–4, 4].
View SolutionDetermine the intervals of monotonicity for the following functions :
f(x)=ex+5xView Solution

